[추천시스템 시리즈]
2021.08.30 - [데이터과학] - [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천
2021.09.01 - [데이터과학] - [추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE
2021.09.08 - [데이터과학] - [추천 시스템] Matrix Factorization (SGD)
2021.09.28 - [데이터과학] - [추천시스템] Alternating Least Square (ALS)를 활용한 Matrix Factorization
2021.10.18 - [데이터과학] - [추천시스템] Multi-Armed Bandit
MAB의 등장 배경은 카지노에 있는 슬롯머신과 관련있다. Bandit은 슬롯머신을, Arm이란 슬롯머신의 손잡이를 의미한다. 카지노에는 다양한 슬롯머신 기계들이 구비되어 있다. 고객들은 경험적으로 각 슬롯머신은 수익률이 제각기 다르며, 또한 한번 잭팟이 터지면 한동안 수익률이 좋지 않음을 알게 되었다. 하지만 고객은 각 슬롯머신의 수익률을 정확히 알 수 없다. 그리고 고객의 돈은 한정되어 있으므로 N번 플레이를 할 수 있다. 그렇다면 어떤 슬롯머신에 어떻게 투자해야 최적의 수익을 얻을 수 있을까? MAB는 슬롯머신 투자를 최적화하기 위해 제안된 방법론이다.

MAB는 강화학습 알고리즘으로 분류되지는 않지만, 강화학습 소개 자료의 처음에 많이 등장한다. 그 이유는 강화학습의 핵심 아이디어인 탐색과 활용(Exploration and Exploitation)을 사용하기 때문이다. MAB에서 탐색(Exploration)이란, 기존에 파악하지 못한 정보를 얻기 위해 새로운 손잡이를 잡아당겨보는 것이다. 반면에, 활용(Exploitation)이란, 기존의 경험과 정보를 바탕으로 수익률이 가장 좋은 손잡이를 선택하는 것을 의미한다. 또한 강화학습에 나오는 보상(Reward)은 여기서 슬롯머신으로 얻는 수익을 나타낸다. 만약 탐색을 너무 적게하면 기존의 편협한 정보만 가지고 잘못된 슬롯머신을 최적이라 판단하여 높은 수익을 얻을 수 없다. 반대로, 탐색을 너무 많이 하면 탐색 비용이 많이 들어 높은 수익을 얻을 수 없다. 즉, 탐색과 활용이 적절하게 이루어져야 최적의 수익을 찾을 수 있다.
[알고리즘 1] Simple Average Method (greedy algorithm)
첫번째 전략은 우선 모든 슬롯머신을 한번씩 다 플레이해보고 가장 수익률이 좋았던 슬롯머신에 몰빵하는 것이다. 누가 봐도 그렇게 합리적이지 못한 방법이라는 것을 알 수 있다. 각 슬롯머신마다 한번씩만 플레이 해봤기 때문이다. 단 한번의 플레이 결과가 그 슬롯머신의 일반적인 수익률을 나타낼 수 없다. 어떤 슬롯머신은 평소와 달리 우연히 그 한번의 플레이에 높은 수익을 냈을 수도 있기 때문이다. 따라서 어떤 슬롯머신이 최고라고 결론짓기 전에 슬롯머신에 대한 정보를 충분히 얻기 위해 좀 더 탐색하는 시간이 필요하다. 즉, 활용(Exploitation)을 하기 전에 좀 더 충분한 탐색(Exploration)이 필요하다. Greedy 알고리즘의 수식은 아래와 같다. 말로하는 것보다 수식으로 보는 게 더 복잡해 보인다. 😂



[알고리즘 2] Epsilon-greedy algorithm
두번째는 첫번째 전략의 한계점인 탐색(Exploration) 부분을 보완한 전략이다. 일정한 확률에 의해 랜덤하게 슬롯머신을 선택하여 탐색하도록 한다. 여기서 ε(epsilon)이 사용자가 지정하는 확률 값이다. 보통 0.1~0.3 정도로 설정한다. 다음 플레이할 슬롯머신을 선택할 때, 1-ε의 확률로는 greedy 알고리즘을 기반하여 선택하고, ε의 확률로는 랜덤하게 선택한다. 그러나 플레이를 많이 하여 이제 수익률이 높은 슬롯머신을 알게 되더라도 처음과 동일한 확률로 다른 슬롯머신을 선택하게 되므로, 최적값으로부터 멀어질 수 있다는 단점이 있다.

Epsilon-greedy Algorithm Pseudo Code

[알고리즘 3] Upper Confidence Bound (UCB)
Epsilon Greedy 알고리즘에서는 랜덤하게 탐색을 수행했다. 하지만 더 좋은 방법으로 탐색할 수 없을까? 어떤 슬롯머신은 최적일 수도 있고 아닐 수도 있다. 하지만 지금까지 플레이한 횟수가 적다면 현재 수익이 적더라도 최적에 대한 가능성을 갖고 있다고 생각하여 그 슬롯머신을 선택하게 만든다. 즉, 현재 어떤 슬롯머신의 수익이 그닥 좋지 않음에도 아직 충분한 플레이를 해보지 않았기 때문에 조금 더 시도하여 숨은 보석을 발굴하도록 하는 방법이다.


[그림7]의 초록색은 기존의 Greedy 알고리즘과 동일하다. 현재까지 누적 수익을 계산하여 이를 선택에 반영하는 활용(Exploitation) 부분이다. 반면에 파란색은 앞서 말한 시도 횟수가 적은 슬롯머신에게 점수를 많이 주어 선택될 수 있도록 한다(Exploration). 분모는 현재까지 슬롯머신 a가 선택된 횟수인데, 이는 선형적으로 증가한다. 분자는 현재까지 전체 슬롯머신의 플레이 횟수에 로그를 취한 것이다. 로그는 처음에는 가파르게 증가하다가 점차 조금씩 증가한다. 분모가 선형적으로 증가하는 반면, 분자는 점차 기울기가 감소하며 증가한다. 따라서, 어떤 슬롯머신의 시도 횟수가 많아질수록 파란색 부분의 값은 작아진다. 파란색에 있는 c는 탐색에 대한 가중치를 얼마나 줄 것인지 정하는 하이퍼파라미터이다.

[그림9]는 Sutton의 "Reinforcement Learning: An Introduction" 책에 나오는 알고리즘 비교 그래프이다. 가로축은 각 알고리즘 별 하이머파라미터들을 의미하고, 세로축은 슬롯머신을 1,000번 플레이 했을 때 평균 수익을 나타낸다. 우리가 이번 포스팅에서 배운 건 빨간색(epsilon-greedy)와 파란색(UCB)이다. 어찌됐든 4개의 알고리즘 중에서 UCB가 가장 높은 수익을 가지는 것을 알 수 있다.
[알고리즘 4] Thomson Sampling: 광고 추천에 적용
톰슨 샘플링(논문)은 Google Analytics와 Netflix에서도 많이 적용하고 있는 알고리즘이다. 주로 광고 배너를 노출하거나 추천 컨텐츠 중에서 선별하여 노출할 때 사용자의 클릭률(CTR:Click Through Ratio)을 예측하는데 활용된다. 앞서 설명한 예시와는 달리 슬롯머신 대신에 광고 배너를 하나의 선택으로 간주하도록 하자. Reward는 사용자의 광고 배너 클릭이다. 앞에서는 기대 수익이 가장 높은 슬롯머신을 찾아다녔다면, 여기서는 사용자의 클릭 확률이 높은 광고 배너를 찾는 문제가 된다. 그리고 톰슨 샘플링은 각 광고 배너의 클릭 확률을 베타 분포로 표현한다 ([그림10] 참고). 그리고 광고 배너 A와 B의 클릭 확률은 서로 다른 확률변수로 간주하여 각각의 베타분포를 따로 가지고 있다. 베타분포의 두 매개변수 𝛼와 β가 무엇인지는 아래에서 설명할 예정이다. (*𝛼, β가 1보다 작을 경우 U자 형태의 분포를 가지게 되는데, 이를 방지하기 위해 𝛼와 β에 1을 더해준다.)

여기서 헷갈릴 수 있는 부분이 있어 부연 설명을 하겠다. '광고 배너 A의 클릭 확률'이 확률변수이므로, 이를 분포 그래프로 그리면 X축이 광고 배너의 클릭 확률이 된다. 분포 그래프를 보면 Y축도 확률값이 되는데, 그러면 X축도 확률이고 Y축도 확률인 된다. 둘다 확률이라 헷갈릴 수 있다! 하지만 Y축은 광고 배너의 클릭 확률이 특정 값일 확률을 의미한다. 예를 들면, X=0.5이면 Y는 광고 배너의 클릭 확률이 0.5일 확률을 의미한다. 헷갈리지 말자!😉
1) 왜 하필 베타분포를 사용할까?
[이유 1] [0,1]의 닫힌 구간을 지원한다.
앞에서도 언급했듯이 톰슨 샘플링 기반의 광고 추천은 분포의 X축을 광고 배너의 클릭 확률로 간주한다. 그리고 확률은 당연히 0과 1 사이의 값이므로, x축의 구간이 [0,1]인 베타분포의 성질이 중요한 것이다. [그림11]을 보면 x축의 양끝이 0과 1인 것을 알 수 있다. 그리고 베타분포의 두 변수인 𝛼와 β가 어떤 값이든 간에 [0,1] 사이에서 분포의 형태가 결정되므로 서로 다른 분포 간 비교에 매우 용이하다.

[이유 2] 두 개의 양수를 가지고 분포를 표현할 수 있다.
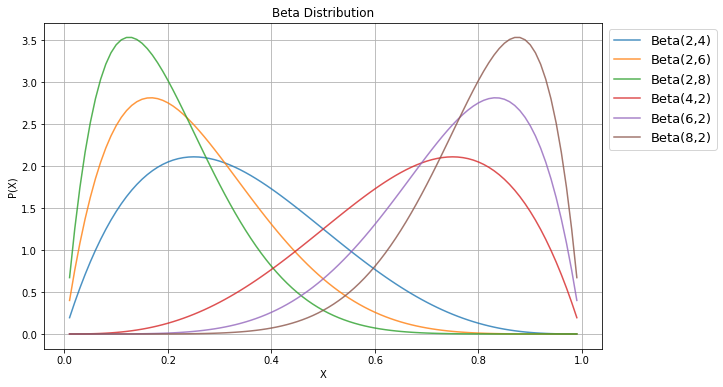
어떤 확률을 베타분포로 표현하기 위해서는 베타분포를 결정짓는 두 매개변수 𝛼와 β에 각각 어떤 수를 대입해야할지 정해야 한다. 그리고 𝛼와 β는 반드시 양수이어야 한다. 광고 추천에서 𝛼는 어떤 광고 배너를 보고 클릭한 횟수를, β는 광고 배너를 보고도 클릭하지 않은 횟수를 사용한다. 왜 𝛼와 β를 이렇게 정하는걸까? [그림11]을 보면 바로 알 수 있다. 왼쪽의 3개 그래프를 보면 𝛼를 고정했을 때 β가 커질수록 왼쪽으로 기울어진 그래프가 형성되는 것을 볼 수 있다. 반면에, 오른쪽 3개 그래프를 보면 β를 고정했을 때 𝛼가 커질수록 오른쪽으로 기울어진 형태를 보인다. 즉, 𝛼가 커지면 광고 클릭 확률이 높도록 분포가 형성되고, β가 클수록 클릭을 안할 확률이 높도록 분포가 형성되는 것이다. 이제 왜 𝛼와 β를 클릭 횟수와 클릭하지 않은 횟수로 정하는지 직관적으로 이해했을 것이다.
2) 예시로 보는 톰슨 샘플링
베타분포를 가지고 각 광고 배너의 클릭 확률 분포를 만든다는 것까지 이해했다면, 이제는 어떻게 그 분포를 업데이트하고 또 추천에 활용하는지 예시를 통해 알아보자. 예시와 세부 과정에 대해 링크에 매우 잘 설명되어 있다. 본 포스팅에서는 해당 예시를 일부만 변형하여 정리하였다.
1단계) 초기 상태: 모든 배너가 동일한 분포를 가짐
두 개의 광고 배너가 있다고 가정하자. 처음에는 모든 배너의 베타분포를 Beta(1,1)로 동일하게 설정한다. 즉, 클릭한 횟수=0, 클릭하지 않은 횟수=0이다. (*𝛼, β가 1보다 작을 경우 U자 형태의 분포를 가지게 되는데, 이를 방지하기 위해 𝛼와 β에 1을 더해준다.)

2단계) 랜덤하게 노출
데이터가 어느정도 쌓일 때까지 랜덤하게 광고를 노출한다. (*보통 각 배너 당 최소 100회씩 노출시키도록 한다. 여기서는 예제이므로 횟수를 적게 하였다.)

3단계) 샘플링하여 노출
랜덤하게 노출한 결과로부터 얻은 마지막 베타분포로부터 각 배너 당 1개씩 샘플링을 한다. 배너1의 샘플값은 0.58이고, 배너2의 샘플값은 0.61이다. 샘플의 값이 더 높은 배너를 노출시킨다. 노출시킨 후 클릭 여부 결과는 다시 베타분포에 반영된다. 이런 과정을 충분히 반복하여 수행해야 한다.

**왜 샘플링을 해야할까?
만약 이 상태에서 샘플링을 하지 않고, 과거 기록만 가지고 선택을 한다면 배너1이 배너2보다 더 많이 클릭됐기 때문에 배너1을 노출할 것이다. 하지만 과거 랜덤하게 노출한 기록만 가지고 무엇이 최선인지 판단하는 것은 이르다. 따라서, 탐색을 더 많이 할 수 있도록 샘플링을 활용하는 것이다.
4단계) 충분한 노출을 거친 후
3단계를 충분히 많은 횟수로 반복하여 수행하면, 어느 순간부터는 각 배너의 분포가 크게 변하지 않는 순간이 올 것이다. 정확한 그 횟수는 정확히 알 수 없으니 말그대로 '충분한 횟수의 노출'을 시키는 것이 중요하다. [그림16]은 배너1이 총 750번, 배너2가 230번 노출된 후 수정된 베타분포이다. 이제 두 분포에서 샘플링을 해도 거의 대부분의 경우에 배너1이 배너2보다 샘플 값이 높게 나타날 것이다. 즉, 배너1의 Reward(CTR: 클릭 확률)가 가장 높다고 결론을 내릴 수 있다.

Thompson Sampling Algorithm Pseudo Code

3) 톰슨 샘플링이 UCB보다 좋을까?
논문에 따르면 톰슨 샘플링이 Regret 측면에서 UCB보다 성능이 우수하다는 것을 실험하여 입증해보였다. 여기서 Regret이란, 현재 시점까지 최적의 선택만해서 얻을 수 있는 Reward와 모델의 선택으로 얻은 Reward 간 차이를 의미한다. 즉, 최적의 선택 대비 우리가 얼마나 잘 선택하고 있는가를 나타낸다. 그러므로 Regret은 작을수록 좋다. [그림17]은 논문에서 실험한 결과 그래프이다. 이에 따르면 4일동안 광고 배너를 추천했을 때 세 가지 알고리즘의 CTR Regret을 그래프로 나타낸 것이다. 톰슨 샘플링이 가장 Regret이 낮은 것을 볼 수 있다. (*Exploit은 탐색 없이 활용만 한 경우를 의미한다.)

Reference
[1] https://brunch.co.kr/@chris-song/62
멀티 암드 밴딧(Multi-Armed Bandits)
심플하고 직관적인 학습 알고리즘 | 강화학습의 정통 교과서라할 수 있는 Sutton 교수님의 Reinforcement Learning : An Introduction 책을 읽어보자. 챕터 1에서는 앞으로 다룰 내용에 대한 개요가 나오며, 챕
brunch.co.kr
[2] http://sanghyukchun.github.io/96/
Machine learning 스터디 (20-1) Multi-armed Bandit - README
들어가며 이 글에서는 reinforcement learning의 한 갈래 중 하나인 Multi-armed Bandit에 대해 다룰 것이다. Multi-armed Bandit이 어떤 문제인지에 대해 간략히 설명한 다음, 좀 더 formal하게 문제를 정의하고, 이
sanghyukchun.github.io
[3] https://web.stanford.edu/class/psych209/Readings/SuttonBartoIPRLBook2ndEd.pdf
[4] https://github.com/bgalbraith/bandits
GitHub - bgalbraith/bandits: Python library for Multi-Armed Bandits
Python library for Multi-Armed Bandits. Contribute to bgalbraith/bandits development by creating an account on GitHub.
github.com
[5] https://github.com/johnmyleswhite/BanditsBook
GitHub - johnmyleswhite/BanditsBook: Code for my book on Multi-Armed Bandit Algorithms
Code for my book on Multi-Armed Bandit Algorithms. Contribute to johnmyleswhite/BanditsBook development by creating an account on GitHub.
github.com
[6] https://brunch.co.kr/@chris-song/66
톰슨 샘플링 for Bandits
밴딧 문제를 해결하는 또 하나의 baseline | 이번 포스팅에서는 톰슨 샘플링에 대해 소개해드리겠습니다. 멀티암드밴딧(MAB) 보다는 좀 더 어려운 확률이론이 나오니, 먼저 대학교 때 기말고사를 보
brunch.co.kr
[7] https://github.com/chris-chris/bandits-baseline/blob/master/beta.py
GitHub - chris-chris/bandits-baseline
Contribute to chris-chris/bandits-baseline development by creating an account on GitHub.
github.com
톰슨 샘플링(thompson sampling)에 대한 직관적인 이해
개요 톰슨 샘플링(thompson sampling)에 대해 공부하여 개념을 이해한 후 핵심을 정리해둔다. 톰슨 샘플링이 왜 좋은가? 톰슨 샘플링을 이해하기에 앞서 과연 이 알고리즘이 내가 공부할 가치가 있는
www.kwangsiklee.com
[9] https://tech.kakao.com/2021/06/25/kakao-ai-recommendation-01/
카카오 AI추천 : 토픽 모델링과 MAB를 이용한 카카오 개인화 추천
글 작성에는 추천팀 sasha.k와 marv.20가 함께해 주셨습니다. 머신러닝에 대한 기초 지식이 있고, 추천 알고리즘에 관심이 있는 분들에게 카카오 추천팀이 개인화 추천 기술을 활용하는 방법에 대해
tech.kakao.com
[10] https://proceedings.neurips.cc/paper/2011/file/e53a0a2978c28872a4505bdb51db06dc-Paper.pdf
'데이터과학' 카테고리의 다른 글
| [머신러닝] 프로젝트 전략 (2): Evaluation Metric (0) | 2022.01.24 |
|---|---|
| [머신러닝] 프로젝트 전략 (1): Orthogonalization (0) | 2022.01.23 |
| [추천시스템] Alternating Least Square (ALS)를 활용한 Matrix Factorization (7) | 2021.09.28 |
| [추천 시스템] Matrix Factorization (SGD) (4) | 2021.09.08 |
| [추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE (2) | 2021.09.01 |




댓글