[추천시스템 시리즈]
2021.08.30 - [데이터과학] - [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천
2021.09.01 - [데이터과학] - [추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE
2021.09.08 - [데이터과학] - [추천 시스템] Matrix Factorization (SGD)
2021.09.28 - [데이터과학] - [추천시스템] Alternating Least Square (ALS)를 활용한 Matrix Factorization
2021.10.18 - [데이터과학] - [추천시스템] Multi-Armed Bandit
본 포스팅에서는 추천 시스템에서 가장 많이 사용되는 Matrix Factorization(이하 MF)에 대해 소개한다. MF는 Collaborative Filtering의 한 종류로, Netflix Prize에서 처음 등장하여 엄청난 성능 향상을 보임으로써 추천 시스템 분야의 혁신을 일으켰다(논문). 기존에 많이 사용되었던 컨텐츠 기반 추천 알고리즘은 Data Sparsity와 Scalibility에 취약했다. MF는 이런 한계점을 극복하면서도 추천 속도가 빨라 현실 세계에서는 가장 많이 쓰인다. 딥러닝이 급부상한 요즘에는 MF의 원리를 딥러닝에 응용하여 성능을 한층 더 높였다고 한다.
1. Matrix Factorization
1) SVD와 MF의 관계
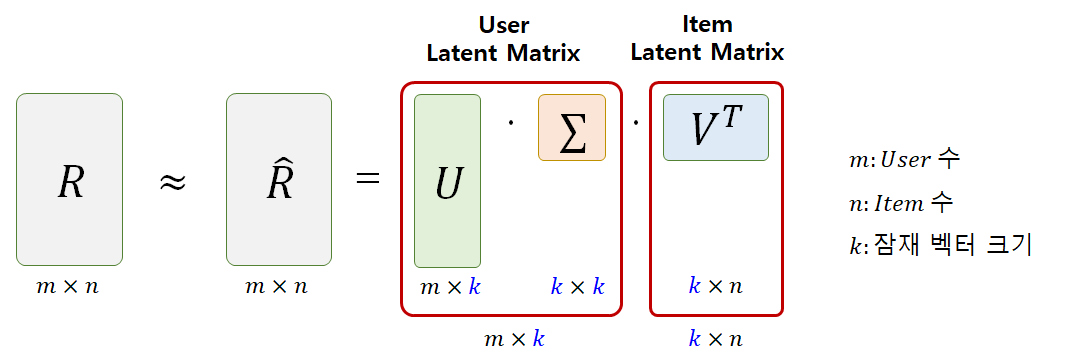
MF는 선형대수학의 SVD(Singular Value Decomposition)을 응용하여 나온 방법론이다. 간단히 말하자면 하나의 행렬을 여러 행렬로 분해한다는 관점을 차용한 것이다. SVD에 대해서는 다른 포스팅을 통해 자세히 다루도록 하겠다. [그림1]을 보면 먼저 Full SVD를 통해 좌측의 행렬 A를 세 개의 행렬로 분해했다. 그 중에서 가운데 행렬은 특이값을 갖고 있는데, 특이값은 클수록 더 많은 정보를 갖고 있다고 해석할 수 있다. 비대각 행렬 부분은 전부 0으로 채워져 있다. 그리고 특이값 중에서도 0인 애들이 있다. 얘네들은 전부 아무런 정보를 갖고 있지 않은 불필요한 값이다. 그러므로 모든 값을 다 사용하는 것보다는 핵심적인 정보만 추려서 사용하는 것이 효율적이다. 그래서 특이값이 높은 상위 K개만 추려서 사용하는데 이를 Truncated SVD라고 한다. 모든 값을 다 사용하는 것이 아니라 적은 정보만으로 A와 근사한 행렬을 도출할 수 있는 것이다.

그럼 이제 MF가 SVD를 어떻게 활용하는지 보자. SVD를 하는 대상 행렬 A가 추천 시스템에서는 User-Item Rating 행렬(R)이다. SVD를 하면 3개의 행렬로 분해되는데 이 중에서 첫 번째와 두 번째 행렬을 내적한 것을 하나의 사용자 잠재 행렬로 생각하고, 마지막 세번째 행렬을 아이템 잠재 행렬로 사용한다. 즉, MF에서는 사용자와 아이템 잠재 행렬 두 가지로 분해하여 사용하는 것이다. 이 때, 잠재 행렬 안에 있는 잠재 벡터의 크기는 K이다. P와 Q의 조합으로 User-Item Rating 행렬의 예측값(R_hat)을 구할 수 있다.
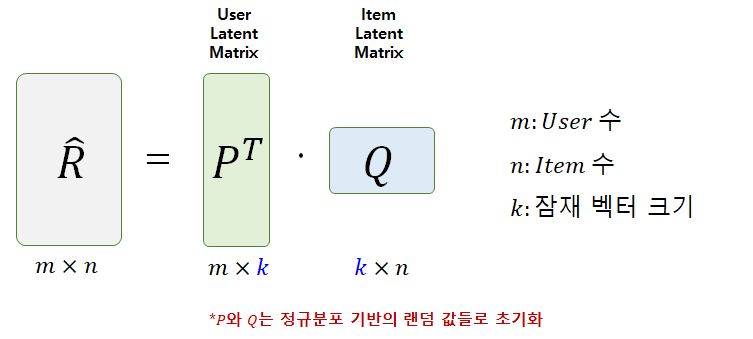
다시 정리해보자. 사용자 잠재 행렬 P (k X m)와 아이템 잠재 행렬 Q (k X n)이 있고, 두 행렬을 내적하여 평점 예측 행렬 R을 만들 수 있다. 사용자 u가 아이템 i에 대한 예측 평점은 [그림4]의 수식으로 표현된다. P와 Q 안에 있는 값들은 모두 학습해야 하는 파라미터들이다. 해당 파라미터들은 학습 시작 전에 (표준)정규분포 기반의 랜덤 값들로 초기화된다.

2) Objective Function
그럼 이제 P와 Q를 학습할 때 사용되는 목적 함수를 소개한다.

1) 오차 제곱 합
목적 함수는 두 가지 텀으로 나뉘는데, 앞 부분은 우리가 많이 알고 있는 SE(Squared Error)와 같다. 여기서 오차란, 실제 평점값과 예측 평점 값의 차이이다. 주목할 점은 학습 데이터에서 실제 평점이 있는 경우(observed)에 대해서만 오차를 계산한다는 것이다. SVD는 행렬 분해를 위해 행렬 안에 값이 모두 차있어야 한다. 그러나 User-Item Rating 행렬의 경우, 사용자는 극히 일부의 아이템에만 평점을 남겨 행렬의 대부분이 결측값으로 존재한다. 즉, Sparsity가 매우 높다. SVD를 사용하려면 결측값을 0이나 평균 평점 등으로 대체해야 하는데, 이는 데이터를 왜곡시키므로 학습에 악영향을 미친다. 반면에, MF는 결측치를 대체하지 않고도 학습이 가능하므로 Sparsity가 성능에 큰 영향을 주지 않는다는 장점이 있다.
2) 정규화
두 번째는 과적합을 방지하는 정규화 텀이다. 모델이 학습함에 따라 파라미터의 값(weight)이 점점 커지는데, 너무 큰 경우에는 학습 데이터에 과적합하게 된다. 이를 방지하기 위하여, 학습 파라미터인 p와 q의 값이 너무 커지지 않도록 규제를 하는 것이 정규화이다. MF에서는 L2 정규화를 사용하였다. 파라미터 값이 커지면 p벡터의 제곱과 q벡터의 제곱 합도 커질 것이고 이는 목적 함수도 커지게 하므로 패널티를 주는 것이다. 람다는 목적 함수에 정규화 텀의 영향력을 어느 정도로 줄 것인지 정하는 하이퍼 파라미터이다. 람다가 너무 작으면 정규화 효과가 적고, 너무 크면 파라미터가 제대로 학습되지 않아서 언더피팅(Underfitting)이 발생한다.
3) Optimazation (SGD)
MF에서는 목적함수를 최소화하는 최적화 기법으로 SGD(Stochastic Gradient Descent)를 활용하였다. 파라미터 업데이트를 위해 목적함수를 p와 q로 편미분한다. [그림5]는 MF의 목적함수(L)을 p와 q로 미분하는 과정을 보여준다. 이렇게 편미분으로 도출된 값을 Gradient라고 한다. (자세한 내용은 아래 <더보기>를 참고 바란다.)
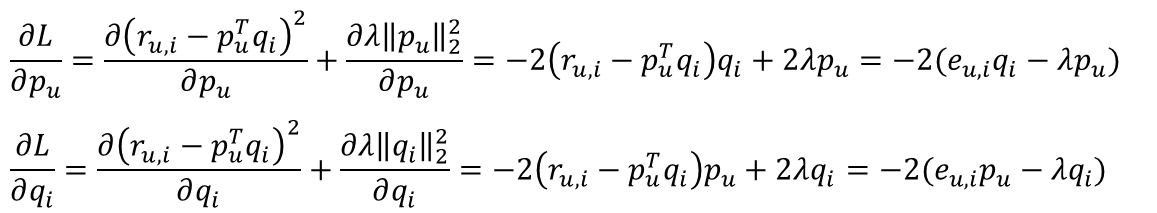
1. 미분
아래는 합성함수 미분의 예시이다. y가 x에 관한 식인 경우, y제곱을 x로 미분하면 2f(x)f'(x)가 된다. MF에서는 오차를 f(x), p 또는 q를 x라고 생각하고 아래 수식을 적용하면 된다.
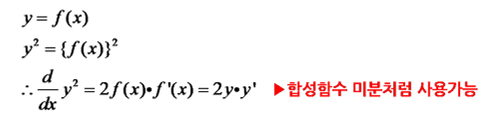
2. Gradient
목적함수(J)를 파라미터(w, weight)로 편미분 하면 목적함수에 대한 파라미터의 기울기(Gradient)를 구할 수 있다. 아래 그림에서 볼 수 있듯이 목적함수 값이 클수록 기울기도 가파른 것을 볼 수 있다. 그리고 Gradient는 벡터로 방향도 가지고 있는데 미분값으로 나온 Gradient는 위를 향하고 있다. 그러나 우리는 더 낮은 곳으로 이동해야하므로 기존 파라미터를 업데이트를 할 때 Gradient를 빼줘야 한다.
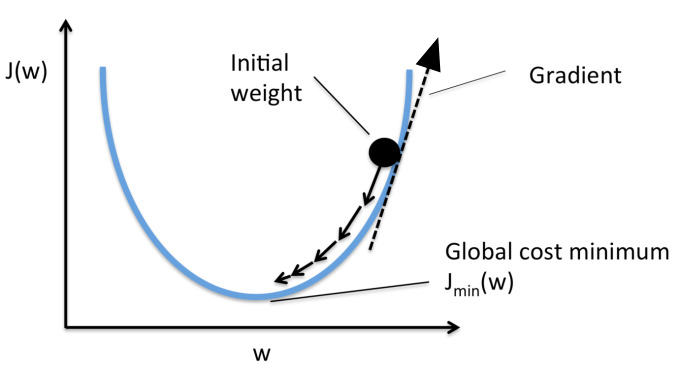
앞서 편미분을 통해 구한 Gradient를 현재 상태의 파라미터 값에서 빼줌으로써 업데이트를 진행한다([그림. 6] 참고). 여기서 에타(η)는 Learning Rate를 의미한다. Learning Rate란, 파라미터를 업데이트 할 때 얼마나 크게 변화시킬지를 정하는 하이퍼 파라미터이다. <더보기>의 Gradient 그림을 보면 weight라는 동그라미가 아래로 이동하는데, 그 이동하는 '보폭'을 얼마나 크게 할 것인가를 정한다고 생각하면 된다.
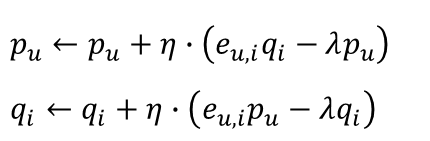
SGD는 모든 사용자(u) 잠재 벡터와 모든 아이템(i) 잠재 벡터에 대해서 파라미터 업데이트를 하나씩 순차적으로 진행된다. 따라서 사용자와 아이템 수가 많아질수록 학습이 매우 오래 걸린다. 그리고 하나씩 순차적으로 학습해야 하다보니 병렬처리가 불가능하다. 이러한 단점을 보완하여 병렬 처리가 가능한 ALS라는 최적화 기법이 등장했다. ALS는 다음 포스팅에서 소개하도록 하겠다.
2. Adding Biases
사용자나 아이템별로 평점에 편향이 있을 수 있다. 예를 들어, 사용자 A는 점수를 후하게 주고 반면에 사용자 B는 점수를 짜게 준다던지, 아니면 어떤 영화는 유명한 명작이라 사용자의 취향과 별개로 점수가 높고, 어떤 영화는 그렇지 않을 수 있다. [그림7]을 보면, Adding Bias에서 예측 평점은 학습 데이터 전체 평점의 평균(μ)에 사용자가 가진 편향(b_u), 아이템이 가진 편향(b_i), 그리고 두 잠재벡터의 내적들로 구성되어 있다. 모든 평점의 평균을 더해주는 이유는 대부분의 아이템이 평균적으로 μ 정도의 값은 받는다는 것을 감안해주기 위함이다.

위의 예측값을 가지고 수정된 목적함수는 아래와 같다. 여기서 주의할 점은, μ는 학습 데이터로부터 도출되는 상수값인 반면에, Bias들은 모두 학습 대상인 파라미터라는 것이다. 따라서, 두번째 정규화 텀에도 Bias가 추가되어 있다. (*참고: p와 u는 벡터인 반면, bias들은 모두 스칼라값이므로 둘이 서로 표현법이 다르다.)

위에서 설명한대로 SGD를 하기 위한 업데이트 공식은 아래와 같이 도출된다([그림9] 참고). 이번에는 파라미터가 네 종류이므로, 4개의 각각 파라미터로 목적함수를 편미분하여 Gradient를 구하고 이를 바탕으로 업데이트를 수행한다. 대체로 기본 MF보다 Adding Bias를 적용했을 때 성능이 더 좋게 나온다.

3. MF의 장점과 단점
MF는 Data Sparsity에 큰 영향을 받지 않는다는 점에서 Content Base Collaborative Filtering(이하 CBCF)이나 SVD보다 성능이 훨씬 좋다. 사용자나 아이템이 늘어날수록 Sparsity가 증가하게 되는데, CBCF나 SVD는 결측값을 임의로 채워서 추천에 사용하다보니 성능이 떨어질 수 밖에 없다. 반면에, MF는 결측값을 아예 사용하지 않으므로 사용자와 아이템이 많아져도 기존 성능을 유지할 수 있다. 즉, Sparsity에 강하고 Scalibility가 좋다. 그러나 SGD를 활용한 MF는 앞서 언급한대로 사용자와 아이템이 많아지면 학습 속도가 느리고, 병렬 처리도 불가능하다는 단점이 존재한다. 앞으로 MF 기반의 개선된 추천 알고리즘에 대해 소개할 예정이다.
References
[1] https://datajobs.com/data-science-repo/Recommender-Systems-[Netflix].pdf
[2] https://darkpgmr.tistory.com/106
[선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용
활용도 측면에서 선형대수학의 꽃이라 할 수 있는 특이값 분해(Singular Value Decomposition, SVD)에 대한 내용입니다. 보통은 복소수 공간을 포함하여 정의하는 것이 일반적이지만 이 글에서는 실수(real
darkpgmr.tistory.com
'데이터과학' 카테고리의 다른 글
| [추천시스템] Multi-Armed Bandit (2) | 2021.10.18 |
|---|---|
| [추천시스템] Alternating Least Square (ALS)를 활용한 Matrix Factorization (7) | 2021.09.28 |
| [추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE (2) | 2021.09.01 |
| [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천 (0) | 2021.08.30 |
| [머신러닝] 앙상블 학습 - 2) Bagging (0) | 2021.06.23 |




댓글