[추천시스템 시리즈]
2021.08.30 - [데이터과학] - [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천
2021.09.01 - [데이터과학] - [추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE
2021.09.08 - [데이터과학] - [추천 시스템] Matrix Factorization (SGD)
2021.09.28 - [데이터과학] - [추천시스템] Alternating Least Square (ALS)를 활용한 Matrix Factorization
2021.10.18 - [데이터과학] - [추천시스템] Multi-Armed Bandit
본 포스팅에서는 Matrix Factorization의 학습 속도를 매우 향상시킨 Alternating Least Square (ALS) 최적화 방법 소개한다. 지난번 포스팅에서 기존의 MF는 SGD를 활용하기 때문에 학습 속도가 느리고 병렬 처리가 불가능하다는 한계점을 언급했었다. 또한, MF는 평점과 같이 사용자가 직접적으로 아이템에 대해 평가를 내린 Explicit Feedback에만 사용이 가능했다. 그러나 대부분의 사용자-아이템 상호작용은 평점처럼 명확하지 않은 경우가 많다. 예를 들어, 쇼핑몰에 접속한 사용자가 어떤 아이템을 클릭했다고 가정하자. 클릭이라는 액션은 아이템에 대한 사용자의 관심의 표현일 수는 있지만 해당 상품을 구매한다는 명확한 시그널은 아니다. 즉, 이런 데이터를 Implicit Feedback이라고 하며, 현실에는 Explicit 보다는 Implicit Feedback 데이터를 바탕으로 추천서비스를 제공해야 하는 경우가 훨씬 많다. 그러면 ALS는 어떻게 이런 문제들을 해결했는지 알아보자(논문).

1. Objective Function & Optimization
ALS의 메인 아이디어는 MF에 사용되는 사용자와 아이템 잠재벡터 이렇게 두 종류의 파라미터를 서로 번갈아가면서 업데이트를 한다는 것이다. 즉, P와 Q 중 하나를 고정해놓고 다른 하나를 업데이트하는 방식이다. 왜 변수 하나를 상수로 고정하는 것일까?
(*Notation이나 MF에 대한 상세 설명은 지난 포스팅을 참고 바람)

[그림2]는 ALS의 목적함수이며 SGD MF와 완전히 동일하다. 그러나 여기서 하나를 상수로 고정한 후 최적화 문제를 풀게 된다면 이는 선형회귀 문제가 된다. 그리고 선형회귀 문제는 SGD와 다르게 주어진 값들을 바탕으로 OLS Formula를 통해 최적의 값을 한번에 도출할 수 있다. 여기서 잠깐 OLS에 대해 살펴보자.
1) OLS를 활용한 단순 선형회귀 최적화
최소자승법(OLS: Ordinary Least Squares)이란, 잔차제곱합(RSS: Residual Sum of Squares)을 최소화하는 가중치(β)를 구하는 방법이다. 이는 회귀계수가 1개인 가장 단순한 선형회귀 문제이다. X는 주어진 데이터, y는 정답이고, β가 바로 우리가 최적화를 위해 알아야하는 변수다. y와 β, X의 구성은 [그림4]와 같다. 그리고 잔차제곱합을 최소화하는 β는 최소자승법(OLS Formula)을 활용하여 바로 구할 수 있다. OLS Formula 유도 과정을 상세히 정리해봤다.


RSS를 풀어서 쓰면 아래와 같다. 두번째 줄에 파란색으로 표시한 부분이 어떻게 세번째 줄에 있는 파란색으로 바뀌는지는 오른쪽에 부가설명을 적어두었다.

RSS를 β로 미분한 값이 0일 때 RSS는 최솟값을 가진다. 그 이유는 RSS가 Convex function이기 때문이다. Convex function이란 국사 시간에 배운 빗살 무늬 토기처럼 아래로 볼록한 형태를 가진 함수를 뜻한다. 어떤 함수를 미분한 값이 0이라는 것은 기울기가 0이라는 뜻이고, Convex function에서 기울기가 0인 곳은 빗살무늬 토기의 가장 아래 꼭지, 즉 함수에서 가장 값이 작은 부분이라는 뜻이다. 그리고 Convex Function에서 기울기가 0인 곳은 유일하다.

따라서, 우리는 RSS를 β로 미분했을 때 0이 되도록 하는 β값을 찾아야 한다. 최적의 β를 찾는 과정은 아래와 같으며, 최종적으로는 복잡한 계산없이 X와 y의 행렬 계산으로 β 도출이 가능함을 알 수 있다.


OLS Formula 유도 과정을 통해 우리는 최적의 파라미터를 단순 계산만으로 쉽게 구할 수 있음을 확인했다. 이러한 방법을 적용하여 SGD의 느린 학습 속도를 개선할 수 있도록 ALS 최적화가 등장했다.
2) ALS를 활용한 최적화
이제 다시 추천 시스템으로 돌아오자. 우리는 변수가 2개 있지만 하나를 현재 상태의 값으로 고정함으로써 상수로 만들었다. 예를 들어, p를 변수라고 생각하면, Q는 현재 우리가 알고 있는 데이터 X처럼 취급하는 것이다. 따라서 기존의 목적함수도 p와 q의 목적함수 두 개로 분리할 수 있다. 그 결과는 아래와 같으며, 각각의 디멘전에 대해 오른쪽에 표기하였다. (기존 목적함수는 앞 텀이 ( ) 괄호로 묶인 후 ∑로 더해졌는데, 아래는 앞텀이 모두 벡터이므로 Notation이 || ||로 바뀌었다.)
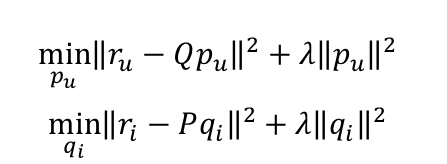
OLS Formula처럼 분리한 두 개의 목적함수에 대해 최적의 p와 q를 찾을 수 있다. 앞서 OLS 예시로 보여준 y, X, β를 ALS에서는 r, Q, p로 대체하면 똑같아진다. 여기서 n은 사용자 수, k는 잠재벡터의 크기이다.

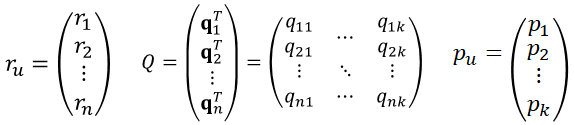
필요한 값들을 정의했으면 이제 OLS 최적화 방법을 적용하여 해를 구하면 된다. 아래 세 단계로 나누어 파라미터 p의 최적값을 찾는 과정을 상세히 정리했다. 수식이 많아 보이지만 앞서 설명한 OLS 유도 과정을 잘 이해했다면 이와 거의 유사하기 때문에 어렵지 않을 것이다. 이 세 단계를 q에도 동일하게 적용하면 [그림7]과 같은 최적해 수식을 유도할 수 있다.

ALS는 아래 두 개의 수식을 가지고 서로 번갈아가면서 업데이트를 하며 최적해를 찾는다. Q를 고정해놓고 p를 업데이트하고, 업데이트한 P를 다시 고정해놓고 q를 업데이트한다. OLS는 Convexity 덕분에 유일하고 가장 작은 목적함수 값을 보장할 수 있다. 따라서, 목적함수는 같거나 작아질수는 있어도 절대 증가하지는 않는다. 업데이트를 진행할수록 목적함수는 작아질 수밖에 없는 것이다.
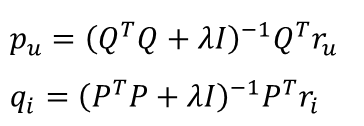
ALS는 SGD와 다르게 각 데이터 포인트를 순차적으로 업데이트할 필요가 없다. 주어진 행렬을 가지고 계산만 하면 되기 때문에 아래 그림처럼 행렬을 쪼개서 병렬 처리가 가능하다. 따라서, ALS가 SGD보다 훨씬 빠른 속도로 학습을 수행할 수 있다.

2. Implicit Feedback
그럼 이제 ALS가 어떻게 Implicit Feedback 데이터를 가지고 추천 서비스를 할 수 있는지 살펴보자. Implicit 데이터는 구체적인 점수가 아니므로 사용자가 아이템에 관심있는지 여부(Preference)를 Binary로 표현하여 사용한다. r은 구매 횟수나 클릭 횟수 등을 의미하고, r이 양수인 경우에는 preference가 1, 그렇지 않으면 0이다. (구매 횟수, 클릭 횟수에 음수 값은 없을 것이다.) 주목할점은 인터랙션이 한번도 없는 경우 Preference값이 음수가 아니라 0이라는 것이다. 어떤 아이템이 아직 사용자에게 노출이 되지 않았거나 어떠한 제약사항으로 인해 인터랙션이 없었을 수도 있기 때문이다.
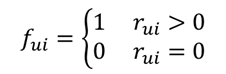
그리고 사용자가 아이템을 얼마나 선호하는지를 나타낸 Confidence 값을 정의한다. 여기서 α는 인터랙션이 있는 경우 r의 중요도를 조절하는 하이퍼파라미터이다. r의 값이 높아질수록 Confidence 값이 증가하게 만든다(Increasing Function). 앞서 언급한 것처럼 인터랙션이 없다고 해서 선호하지 않는 것이 아니므로 이런 경우에는 낮은 Confidence 값을 가진다. 여기서 r은 이미 알고 있는 값이고, α는 사용자 설정값이므로 Confidence는 상수가 된다. 즉, 학습대상이 아니다.
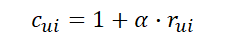
Preference와 Confidence를 반영하여 새로운 목적 함수를 정의한다. 영화 평점인 경우 정답이 1~5점이지만, 여기서는 정답이 Binary Value이다. 따라서 Implicit Feedback에서는 예측값이 0~1 사이가 되도록 학습된다. 그리고 그 값은 평점이 아니라 사용자가 어떤 아이템에 대해 갖는 선호도를 의미한다.
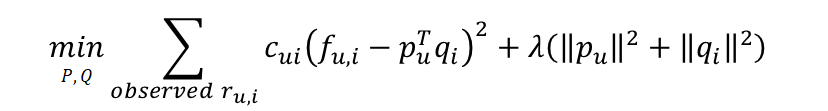
최적화 방법은 SGD나 ALS 모두 가능하다. 여기서는 ALS를 활용한 업데이트 수식을 정리하였다. 앞에서 배운 ALS 업데이트 수식과 비교해보면, 상수값인 C가 추가되었고 r이 f로 바뀐 것뿐이니 이해하는데 어렵지 않을 것이다. 유도 과정은 생략한다.
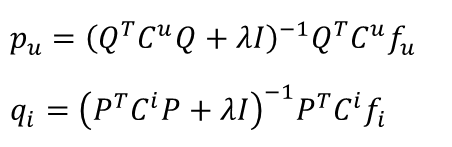
추가로 Implicit Feedback 기반 추천 서비스의 경우, 보통 Top K 아이템을 추천하고 관련 성능 평가 지표를 활용한다(Precision, Recall, NDCG, Hit Rate 등). 반면에 Explicit Feedback 기반 추천 서비스의 경우 MAE나 RMSE를 사용한다. 성능 평가 방법은 포스팅에 자세히 정리해두었다.
3. ALS의 장점과 단점
ALS는 분산처리가 가능하여 학습 속도가 매우 빠르다. 또한 Sparse한 데이터에 대해 SGD보다 강건(Robust)한 모습을 보인다. Implicit Feedback의 경우 Explicit Feedback보다 더 Sparse한 경향이 있다. 따라서 Implicit Feedback에는 SGD보다 ALS를 사용하는 것이 유리하다.
References
[1] http://yifanhu.net/PUB/cf.pdf
[2] https://yeo0.github.io/data/2019/02/23/Recommendation-System_Day8/
Matrix Factorization에 대해 이해, Alternating Least Square (ALS) 이해
Recommendation System_Day8
yeo0.github.io
[3] https://omicro03.medium.com/linear-regression-63164cd2e51
Linear Regression
선형회귀 알고리즘
omicro03.medium.com
[4] https://bladejun.tistory.com/84
ALS 알고리즘
해당 Alternative Least Squares 알고리즘은 Collaborative Filtering for Implicit Feedback Datasets 논문을 기반으로 설명을 드리도록 하겠습니다. ALS알고리즘은 MF(matrix factorization)을 통해 나온 user-l..
bladejun.tistory.com
[5] https://yamalab.tistory.com/89
[Recommender System] - MF(Matrix Factorization) 모델과 ALS(Alternating Least Squares)
추천 알고리즘 중에 가장 널리 사용되는 알고리즘은 단연 CF이다. 그중에서도 단일 알고리즘으로써 가장 성능이 높은 것은 단연 Model Based CF인 Matrix Factorization 계열의 알고리즘이다. (CF 기반 모델
yamalab.tistory.com
'데이터과학' 카테고리의 다른 글
| [머신러닝] 프로젝트 전략 (1): Orthogonalization (0) | 2022.01.23 |
|---|---|
| [추천시스템] Multi-Armed Bandit (2) | 2021.10.18 |
| [추천 시스템] Matrix Factorization (SGD) (4) | 2021.09.08 |
| [추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE (2) | 2021.09.01 |
| [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천 (0) | 2021.08.30 |




댓글