[추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE

[추천시스템 시리즈]

이번 포스팅에서는 대표적인 추천시스템의 성능 평가 방법들을 소개한다. 평가에는 여러가지 관점이 있을 수 있다. 비즈니스나 서비스 관점에서는 추천 모델의 정확도보다는 추천시스템을 적용함으로써 매출이나, 클릭률이 얼마나 증가하는가가 주요 관심사일 것이다. 품질 관점에서는 연관성이나 다양성, 새로움, 참신함 등을 기준으로 평가한다. 그러나 본 글에서는 모델링을 하는 개발자의 관점에서 오프라인으로 테스트 시 사용하는 평가 지표를 소개한다. 우선 모델이 오프라인 테스트에서 좋은 성능을 보여야 온라인 테스트(A/B 테스트)를 진행할 수 있기 때문이다. 평가 지표는 크게 아래 두 가지 그룹을 나눌 수 있다.

1) Ranking 기반 추천 시스템: Precision/Recall@K, NDCG@K, Hit Rate

2) 평점 예측 기반 추천 시스템: MAE, RMSE

1. Precision/Recall@K

머신러닝 평가 지표로 많이 사용되는 Precision, Recall을 의미하는 것이 맞다. 그런데 뒤에 @K가 붙었다. 기존의 Precision, Recall은 Binary classification에 사용되지만, 추천시스템은 하나의 아이템만 추천하지 않으며 정답도 여러개가 될 수 있다. 따라서 등장한 것이 바로 K다. K는 추천 아이템 수를 의미한다. (뒤에서 소개할 모든 평가 방법의 K는 동일하다.)

1) Precision@K

Precision은 내가 1로 예측한 것 중에 실제 1이 얼마나 있는지 비율을 나타낸다. Precision@K는 내가 추천한 아이템 K개 중에 실제 사용자가 관심있는 아이템의 비율을 의미한다. [그림1]의 예시에 따르면, 추천한 아이템은 5개, 추천한 아이템 중에서 사용자가 좋아한 아이템은 3개다. 따라서, Precision@5=0.6이 된다.

2) Recall@K

Recall은 실제 모든 1 중에서 내가 1로 예측한 것이 얼마나 되는지 비율을 나타낸다. Recall@K는 사용자가 관심있는 모든 아이템 중에서 내가 추천한 아이템 K개가 얼마나 포함되는지 비율을 의미한다. [그림1]의 예시를 보면, 사용자가 좋아한 모든 아이템이 6개, 그 중에서 나의 추천에 포함되는 아이템이 3개다. 따라서, Recall@5=0.5가 된다.

2. Mean Average Precision@K

앞서 설명한 Precision@K, Recall@K는 모두 순서를 신경쓰지 않는다. 하지만 추천 시스템에서는 사용자가 관심을 더 많이 가질만한 아이템을 상위에 추천해주는 것이 매우 중요하다. 이를 위해 성능 평가에 순서 개념을 도입한 것이 Mean Average Precision@K 이다. 여기서 Mean과 Average가 모두 한국어로 번역하면 평균이므로 혼란스러울 수 있다. 정확하게는 Average Precision의 Mean으로 해석해야 한다. 우선 Average Precision이 무엇인지부터 살펴보자.

1) Average Precision@K

Precision@i는 추천한 아이템 개수 K중에서 해당 인덱스까지만 고려했을 때의 Precision 값이다. 예를 들어, Precision@1은 가장 처음에 나오는 아이템을 하나만 추천했을 때의 Precision 값이다. [그림2]의 예시를 보면, User A는 가장 처음에 추천한 아이템 A를 좋아했으므로 Precision@1의 값은 1/1=1이고, Precision@2는 1/2이다.

rel(i)는 relevence를 나타내는데, 해당 아이템을 사용자가 좋아했는지 여부를 나타낸다. (0 또는 1 값을 가진다.) Precision에 relevence 값을 곱해주는 이유는 정답 아이템이 추천 목록 중에서 딱 해당 순위에만 영향력을 주도록 하기 위함이다. 정답이 1개 있다고 가정했을 때 똑같이 3개의 아이템을 추천했어도, 정답을 첫 번째로 추천한 경우가 두번째, 또는 세번째에 추천한 것보다 AP 점수가 높아진다.

만약 K가 3이라면, Precision@1*rel(1) + Precision@2*rel(2) + Precision@3*rel(3) 각각을 구해서 더해야 한다. [그림3]의 m은 모든 아이템 중에서 사용자가 좋아한 아이템 수이다. [그림2]를 보면, User A와 User B 둘 다 전체 아이템 중 2개를 좋아했고, 하나가 추천 목록에 포함된다. 그러나 사용자가 좋아한 아이템의 추천 순서가 높았는지 낮았는지에 따라 AP값이 크게 차이난다. User A는 첫번째에 맞췄기 때문에 User B에 비해 점수가 훨씬 높다. 이렇듯 순서를 평가 지표에 반영한 것이 AP이다.

2) Mean Average Precision@K

MAP@K는 모든 유저에 대한 Average Precision@K의 평균을 의미한다. U는 User 집합을, |U|는 유저의 수를 나타낸다. [그림2]의 예시에서 총 사용자가 2명이라고 가정하면, 각 User의 AP@K값의 평균을 하면 MAP@K를 구할 수 있다.

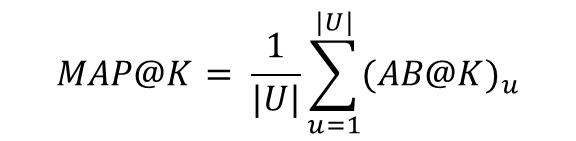
3. NDCG@K (Normalized Discounted Cumulative Gain)

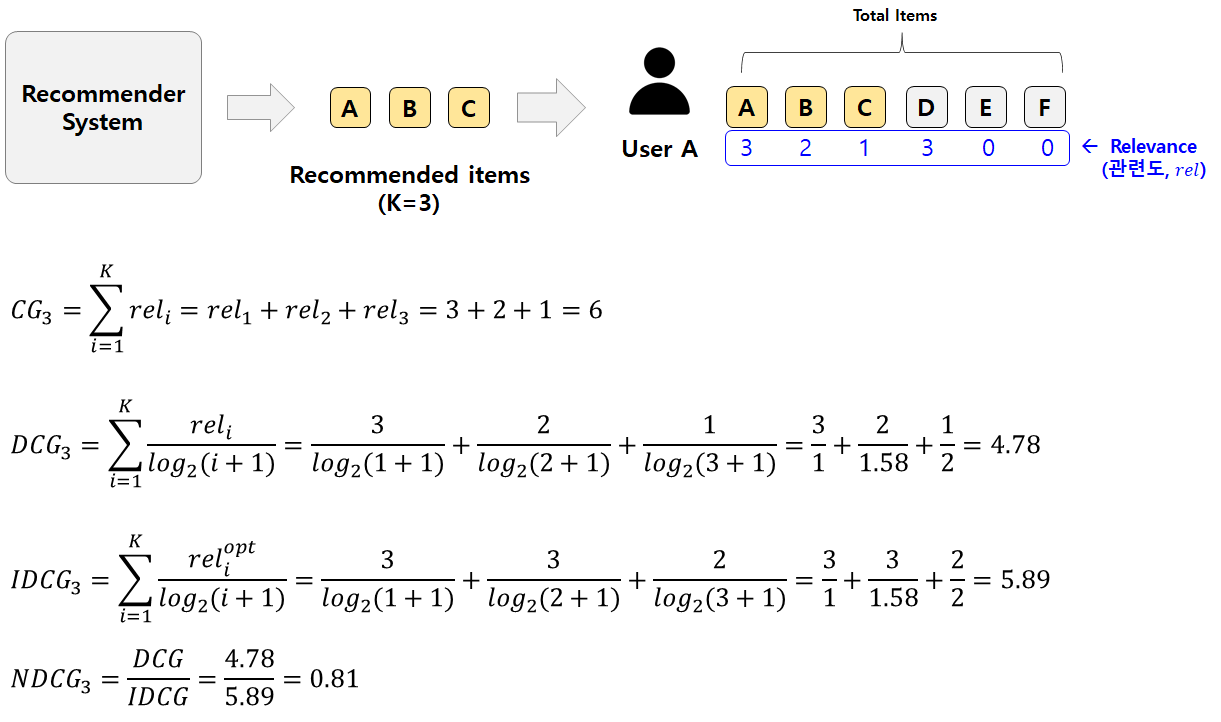
NDCG는 원래 검색 분야에서 등장한 지표이나 추천 시스템에도 많이 사용되고 있다. 위의 두 평가 지표와 마찬가지로 Top K개 아이템을 추천하는 경우, 추천 순서에 가중치를 두어 평가한다. NDCG@K값은 1에 가까울수록 좋다. MAP는 사용자가 선호한 아이템이 추천 리스트 중 어떤 순서에 포함되었는지 여부에 대해서 1 or 0으로만 구분하지만, NDCG@K는 순서별로 가중치 값(관련도, relevance)을 다르게 적용하여 계산한다. [그림4]의 예시를 통해 하나씩 살펴보자.

1) Relevance란?

Relevance란, 사용자가 특정 아이템과 얼마나 관련이 있는지를 나타내는 값이다. Relevance값은 정해진 것이 아니고 추천의 상황에 맞게 정해야 한다. 예를 들어, 신발 추천인 경우 사용자가 해당 신발을 얼마나 클릭했는지, 혹은 클릭 여부(Binary) 등 다양한 방법으로 선정할 수 있다. [그림4]의 예시에서는 전체 아이템에 대한 Relevance를 파란색으로 표시해두었다.

2) Cumulative Gain (CG)

CG는 추천한 아이템의 Relevance 합이다. 두 추천 모델이 순서에 관계없이 동일한 아이템 셋을 추천한 경우 두 모델의 CG는 같아진다. 즉, 순서를 고려하지 않은 값이다.

3) Discounted Cumulative Gain (DCG)

CG에 순서에 따른 할인 개념을 도입한 것이 DCG이다. 추천 아이템의 순서가 뒤에 있을수록 분모가 커짐으로써 전체 DCG에 영향을 적게 주도록 한다. 그러나 사용자별로 추천 아이템의 수가 다른 경우 정확한 성능 평가가 어렵다는 한계점이 존재한다. 예를 들어, 쇼핑몰에서 클릭한 신발 수가 5개인 사용자와 50개인 사용자에게 추천되는 아이템의 수는 다를 수밖에 없다. 추천 아이템의 수가 많아질수록 DCG값은 증가하기 때문에, 정확한 평가를 위해서는 Scale을 맞출 필요가 있다.

5) Normailzed DCG (NDCG)

앞서 말한 DCG의 한계점을 보완하기 위해 DCG에 정규화를 적용한 것이 NDCG이다. [그림7]의 NDCG 수식을보면 정규화를 위해 DCG를 IDCG로 나누는 것을 볼 수 있다. 그럼 IDCG란 무엇일까?

[그림8] Normalized Discounted Cumulative Gain

Ideal DCG (IDCG) 란?

IDCG는 최선의 추천을 했을 때 받는 DCG값이다. IDCG는 모든 추천 아이템 조합 중에 최대 DCG값과 동일하다. [그림4]의 예시에서 가장 이상적인 경우는 Relevance가 높은 순서대로 A(3), D(3), B(2) 이렇게 3개를 추천해주는 것이다. A, D, B를 추천했을 때 DCG값을 구하면 5.89이다.

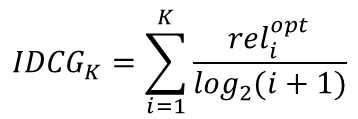
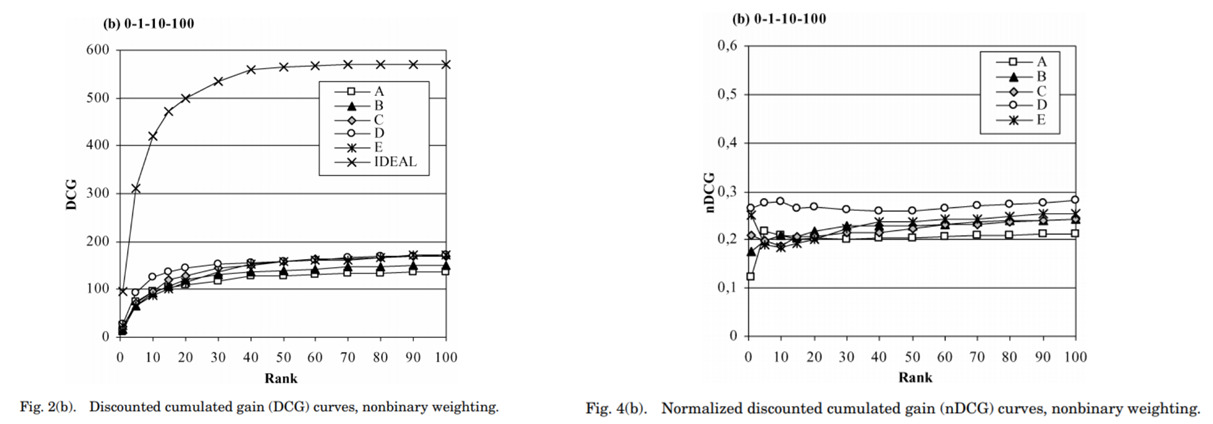
결론적으로, NDCG@K는 가장 이상적인 추천 조합 대비 현재 모델의 추천 리스트가 얼마나 좋은지를 나타내는 지표이다. 그리고 정규화를 함으로써 NDCG는 0~1사이의 값을 가지게 된다. [그림9]는 K(x축, Rank)가 증가함에 따라, DCG과 NDCG가 어떻게 달라지는지 나타낸 그래프이다. 좌측 그래프는 서로 다른 추천 모델(A~E, Ideal)의 DCG값이고, 우측은 NDCG값을 나타낸다. DCG는 K가 증가함에 따라 지속적으로 증가하는 반면, NDCG는 어느정도 K에 독립적이어서 어떤 K가 적절한지 판단이 가능하다. 또한 NDCG가 작은 스케일을 가지기 때문에 비교가 더 용이하다.

4. Hit Rate@K

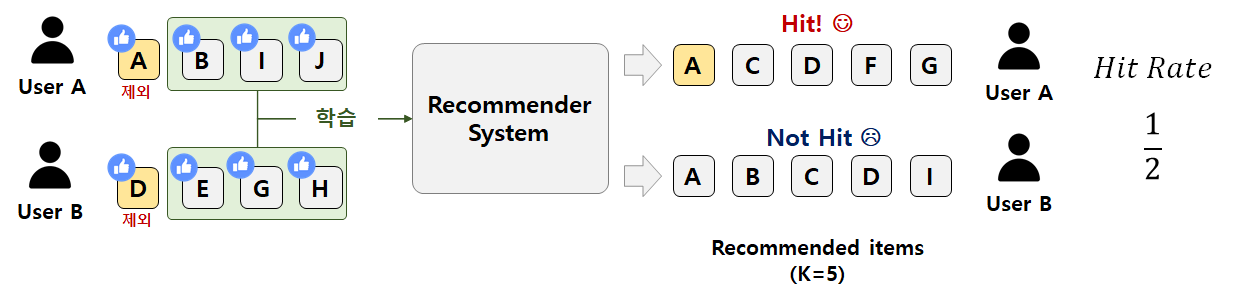
Hit Rate는 전체 사용자 수 대비 적중한 사용자 수를 의미한다(적중률). Hit Rate는 아래 4가지 단계로 구할 수 있다. [그림11]의 예시를 보면 쉽게 이해할 수 있을 것이다.

1) 사용자가 선호한 아이템 중 1개를 제외한다.

2) 나머지 아이템들로 추천 시스템을 학습한다.

3) 사용자별로 K개의 아이템을 추천하고, 앞서 제외한 아이템이 포함되면 Hit이다.

4) 전체 사용자 수 대비 Hit한 사용자 수 비율을 구하면 Hit Rate가 된다.

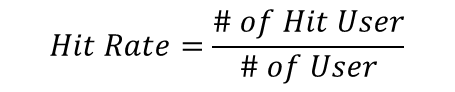
5. MAE & RMSE

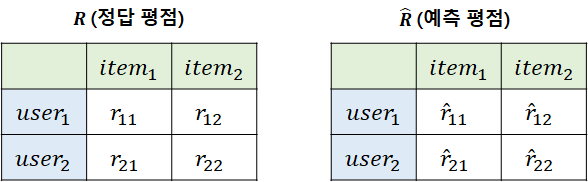
MAE와 RMSE는 앞서 소개한 성능 지표와 달리 '평점 예측'에 대한 평가 방법이다. [그림12]와 같이, 사용자별 아이템에 대한 정답 평점과 예측 평점이 있을 때 두 평점 간 차이를 바탕으로 성능을 평가하는 방법이다.

[그림12] 정답 Rating Matrix와 예측 Rating Matrix

1) MAE (Mean Absolute Error)

MAE는 정답 평점과 예측 평점 간 절대 오차에 대해서 평균을 낸 것이다. MAE의 장점은 직관적이고 해석이 용이하다는 것이다. 그러나 오차가 큰 이상치에 쉽게 영향을 받는다는 단점이 있다.

2) RMSE (Root Mean Square Error)

RMSE는 오차 제곱의 평균을 내고 루트를 취한 것이다. MSE(Mean Sqaured Error)는 제곱으로 인해 단위가 커지는데, 루트를 씌움으로써 실제 예측갑과 유사한 단위를 가지도록 만든다. 또한, MSE는 제곱을 하기 때문에, 1미만인 오차는 더 작아지고 그 이상의 잔차는 더 크게 반영된다. 따라서, 오차의 왜곡현상이 발생하는데 루트를 통해서 이를 완화시켜준다. RMSE는 미분이 가능하다는 점에서 다른 머신러닝 학습에서도 많이 사용되므로 추후 포스팅에서 자세히 다루도록 하겠다.

References

[1] https://velog.io/@redgem92/%EC%B6%94%EC%B2%9C%ED%99%94-%EC%8B%9C%EC%8A%A4%ED%85%9C-04.-%EC%B6%94%EC%B2%9C-%EC%8B%9C%EC%8A%A4%ED%85%9C%EC%9D%98-%ED%8F%89%EA%B0%80-%EC%A7%80%ED%91%9C#normailzed-discounted-cumulaitve-gainndcg

추천화 시스템 04. 추천 시스템의 평가 지표

'데이터과학' 카테고리의 다른 글

[추천시스템] Alternating Least Square (ALS)를 활용한 Matrix Factorization (6)	2021.09.28
[추천 시스템] Matrix Factorization (SGD) (4)	2021.09.08
[추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천 (0)	2021.08.30
[머신러닝] 앙상블 학습 - 2) Bagging (0)	2021.06.23
[머신러닝] 앙상블 학습 - 1) 배경 (2)	2021.06.14

책 읽는 성키

[추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE

1) Ranking 기반 추천 시스템: Precision/Recall@K, NDCG@K, Hit Rate

2) 평점 예측 기반 추천 시스템: MAE, RMSE

1. Precision/Recall@K

1) Precision@K

2) Recall@K

2. Mean Average Precision@K

1) Average Precision@K

2) Mean Average Precision@K

3. NDCG@K (Normalized Discounted Cumulative Gain)

1) Relevance란?

2) Cumulative Gain (CG)

3) Discounted Cumulative Gain (DCG)

5) Normailzed DCG (NDCG)

Ideal DCG (IDCG) 란?

4. Hit Rate@K

5. MAE & RMSE

1) MAE (Mean Absolute Error)

2) RMSE (Root Mean Square Error)

References

'데이터과학' 카테고리의 다른 글

댓글

티스토리툴바

[추천시스템] 성능 평가 방법 - Precision, Recall, NDCG, Hit Rate, MAE, RMSE

1) Ranking 기반 추천 시스템: Precision/Recall@K, NDCG@K, Hit Rate

2) 평점 예측 기반 추천 시스템: MAE, RMSE

1. Precision/Recall@K

1) Precision@K

2) Recall@K

2. Mean Average Precision@K

1) Average Precision@K

2) Mean Average Precision@K

3. NDCG@K (Normalized Discounted Cumulative Gain)

1) Relevance란?

2) Cumulative Gain (CG)

3) Discounted Cumulative Gain (DCG)

5) Normailzed DCG (NDCG)

Ideal DCG (IDCG) 란?

4. Hit Rate@K

5. MAE & RMSE

1) MAE (Mean Absolute Error)

2) RMSE (Root Mean Square Error)

References

'데이터과학' 카테고리의 다른 글

관련글

댓글

티스토리툴바