이번 포스팅에서는 모델의 편향과 분산을 줄이기 위한 노력의 일환인 앙상블 학습에 대하여 정리해봤다. 본 글에서는 1) 앙상블의 목적, 2) 앙상블의 핵심 가치, 그리고 3) 앙상블의 효과를 차례대로 설명한다. 이는 고려대학교 강필성 교수님의 비즈니스 애널리틱스 강의 내용을 요약한 것이며, 해당 강의는 유튜브에서 무료로 시청이 가능하다(링크).
1. 앙상블의 목적

지난 번 포스팅을 통해 편향과 분산의 정도를 바탕으로 모델을 4가지 유형으로 나눌 수 있음을 배웠다. 네 번째 유형(낮은 편향, 낮은 분산)이 가장 바람직한 모델이지만, 현실은 대부분 두 번째나 세 번째인 경우가 많다. 따라서, 이 두 가지 유형에서 네 번째 유형의 모델로 만들기 위한 노력이 바로 앙상블 학습인 것이다. 즉, 앙상블의 목적은 다중 학습 모델을 기반으로 분산 또는 편향 감소를 통해 전체 에러를 줄이는 것이다. 앙상블의 두 종류인 Bagging과 Boosting은 감소하고자 하는 목적이 무엇인지에 따라 구분된다. Bagging은 분산, Boosting은 편향을 줄임으로써 성능을 향상시킨다.
2. 앙상블의 핵심 가치
앙상블의 핵심 가치로는 크게 두 가지가 있는데, 첫 번째가 두 번째에 비해 매우(x100) 중요하다! 따라서 1번 가치를 중심으로 설명하도록 하겠다.
1) 개별 학습 모델들이 충분한 수준의 '다양성(Diversity)'을 가지도록 한다.
2) 개별 학습 모델들의 결과물을 잘 결합한다.
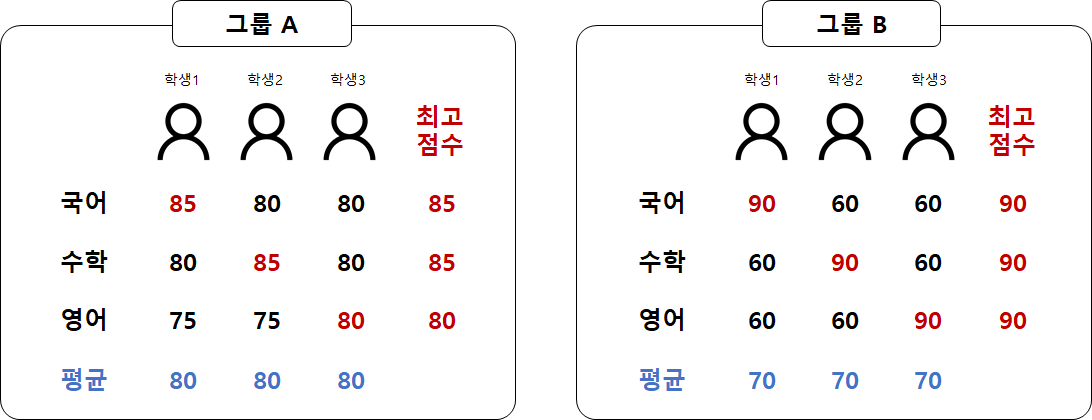
다양성을 추구하는 이유는, 각 개별 모델이 전체 데이터에 대한 성능은 조금 떨어지더라도 특정 분야에 대해 뛰어나다면, 이들을 결합함으로써 전체 성능을 향상시킬 수 있다는 가정 때문이다. [그림 2]의 그룹 A는 그룹 B에 비하여 각 학생들의 평균 점수가 높으며, 각 과목별 학생들간의 점수 차이가 크지 않다. 즉, 학생 간의 다양성이 크지 않다. 반면에 그룹 B는 각 학생들의 평균 점수는 낮지만, 학생별로 주력 과목이 서로 다르며 점수가 매우 높다. 각 그룹의 학생들이 팀이 되어 국영수 시험을 본다고 하면 이들의 최종 시험 결과는 빨간색 글씨(최고점수)가 될 것이다. 학생 개인의 점수는 그룹 A가 뛰어났을지 모르나, 팀의 결과는 그룹 B가 좋은 것이다. 앙상블이 추구하는 것도 바로 이것이다. 서로 다른 분야에서 뛰어난 개별 학습 모델을 결합하여 전체 성능을 높이는 것이다.
앙상블을 구성하는 개별 학습 모델의 다양성을 확보하되, 그렇다고 서로 너무 다르기만 해서는 안된다. 각 학습 모델들의 성능도 어느정도는 보장되어 있어야 한다. 예를 들어, 일반 시사 상식 퀴즈 대회에 나간다고 했을 때 다양한 전공 학과의 대학생 30명 그룹과, 다양한 학년의 초등학생 30명이 대결한다고 하면 일반적으로 대학생 그룹이 정답 확률이 높을 것이다. 아무리 다양한 조합의 앙상블 모델이라해도, 개별 모델의 성능이 너무 떨어지는데 전체 성능이 기적처럼 높아질리는 없다는 뜻이다.
3. 앙상블의 효과
앙상블의 효과를 증명하기 위해, 개별 모델들의 평균적인 에러보다 앙상블의 에러 기댓값을 비교하여 어느 것이 더 낮은지를 확인해보자. [그림 3]을 보면, 앙상블을 위한 개별 모델의 추정치는 정답과 개별 모형의 에러로 구성되어 있다.

그러면 개별 모형들의 에러의 기댓값은 [그림 4]와 같다. 간단히 설명하자면, 모형 m의 추정값(y_m(x))에서 정답(f(x))을 뺀 것의 제곱의 기댓값, 즉, 에러 제곱의 기댓값이다.
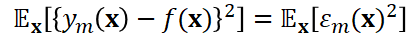
개별 모델 VS 앙상블 모델
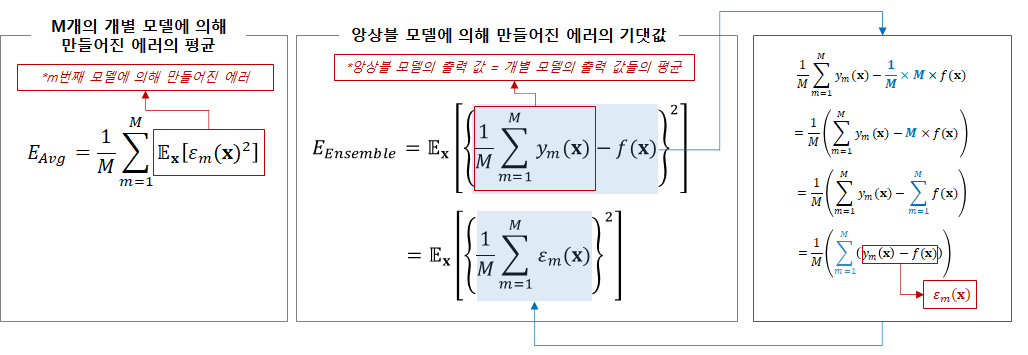
그렇다면 이제 M개의 개별적인 모델에 의해 만들어지는 평균적인 에러와, 앙상블을 통해 만들어지는 에러의 기댓값을 비교해보도록 하자. 첫번째로, E_Avg는 M개의 개별 모델에 의해 만들어진 에러의 평균을 의미한다. E_Ensemble은 앙상블 모델에 의해 만들어진 에러의 기댓값이다. 앙상블은 가장 단순한 방법으로 개별 모델의 추정치(y_m(x))의 평균을 결과값으로 내뱉는다. E_Ensemble이 도출되는 과정은 오른쪽 파란색 박스에 한 단계씩 정리해두었다.
이제 두 경우의 에러를 아래의 최상의 조건과 현실의 조건 두 가지 경우에 나누어 비교해보자.
1) 최상의 조건에서는 앙상블 모델의 에러가 개별 모델의 평균 에러보다 M분의 1만큼 작다.
최상의 조건은 아래의 두 가지를 만족하는 경우를 가정한 것을 의미한다. 첫번째는 개별 모델의 에러의 기댓값이 0인 것(zero mean)이고, 두번째는 각 에러들은 서로 독립적이라는 것(uncorrelated)이다. 이를 수식으로 표현하면 [그림 6]과 같다.

이런 가정하에, E_Ensemble과 E_Avg의 관계를 도출해보면 [그림 7]과 같다. 도출 과정은 아래 상세히 적어두었다. 결과를 해석해보면 앙상블 모델의 에러가 개별 모델의 평균 에러보다 모델의 개수인 M분의 1만큼 작다는 것을 알 수 있다.

2) 현실에서는 앙상블의 에러가 개별 모델의 평균 에러보다 작거나 같음을 보장한다.
그러나 현실의 데이터셋에는 에러들이 서로 독립적인 경우가 잘 없을 것이다. 하지만 다행스럽게도(?), 앙상블은 에러가 상관성이 있다(errors are correlated)는 가정하에도 여전히 성능 유지 또는 향상을 보장한다. [그림 8]은 이를 유도하는 수식이며, 결과를 보면 앙상블의 에러가 개별 모델의 평균 에러보다 항상 작거나 같음을 알 수 있다. 그리고 일반적으로 개별 모형의 최고(single best model)보다 더 나은 성능을 보인다.

여기서 빨간색 박스는 코시-슈바르츠 부등식을 활용한 부분이다. 코시-슈바르츠 부등식의 공식은 아래의 [그림 9]를 참고하기 바란다. [그림 8]에서 1과 epsilon(x)가 [그림 9]의 a와 x의 자리를 대신한다.

4. 마치며
이번 포스팅에서는 앞으로 배울 여러 앙상블 학습 기법이 나오게 된 배경과 목적, 효과를 증명하는 이론에 대해서 배웠다. 이어지는 포스팅에서는 앙상블의 한 종류인 Bagging의 개념과 대표적인 Bagging 모델인 Random Forest에 대해서 정리할 것이다.
References
[1] https://www.youtube.com/watch?v=mZwszY3kQBg
'데이터과학' 카테고리의 다른 글
| [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천 (0) | 2021.08.30 |
|---|---|
| [머신러닝] 앙상블 학습 - 2) Bagging (0) | 2021.06.23 |
| [머신러닝] 편향과 분산의 의미 (1) | 2021.06.04 |
| [머신러닝] 편향-분산 분해 (Bias-Variance Decomposition) (2) | 2021.05.29 |
| [통계] 커널 밀도 추정 (Kernel Density Estimation) (4) | 2021.04.27 |




댓글