본 작성글은 고려대학교 강필성 교수님의 비즈니스 애널리틱스 강의 내용을 바탕으로 정리한 내용이다. 해당 강의는 유튜브에서 무료로 시청이 가능하다(링크). 앙상블 학습(Ensemble Learning)에 대해 순차적으로 다룰 예정이며, 이번 게시글에는 이론적 배경이 되는 편향-분산 분해에 대하여 먼저 알아보도록 한다.
1. Additive Error Model
Additive Error Model이란 데이터에 대한 가정을 의미한다. 우리에게 주어진 현실 세계의 데이터에는 데이터를 생성하는 정답 매커니즘(f(x))이 있다하더라도, 노이즈(epsilon)가 반드시 포함되어 있다는 가정이다. 노이즈란, 사람이 컨트롤 할 수 없는 자연발생적인 변동성을 의미한다. 아래 수식은 Additive Error Model를 설명하는 수식이다(그림 1).
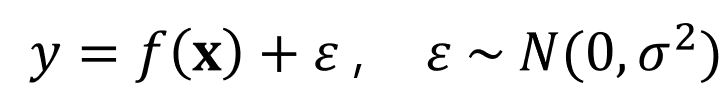
여기서 f 함수는 우리가 찾으려고 하는, 즉 학습시키고자 하는 함수이며 대부분 알려져 있지 않다. 따라서, 우리는 정답 f 함수에 가깝게 y를 뱉어낼 수 있는 f_hat 함수를 찾고자 학습을 수행하는 것이다. 노이즈는 독립적이고 동일한 분포(iid, independent and identically distributed)로부터 만들어졌다고 가정한다. 위 수식에서는 평균이 0이고, 분산이 sigma^2 인 정규분포를 따른다고 가정한다. 편향-분산 분해의 배경에는 Additive Error Model의 가정이 전제되어 있다.
2. 개념 정리
편향-분산 분해 유도 과정에 들어가기 전에, 이해를 돕기 위해 주요한 개념과 용어를 정리해보았다(그림2). 작성자도 공부를 하다 보면 표기법(Notation)을 정확히 몰라서 이해가 잘 안되는 경우가 많았기 때문에 꼭 포함해야 한다고 생각했다. 아래 내용을 기반으로 그림3과 편향-분산 분해 과정을 보면 더욱 이해가 쉬울 것이다.
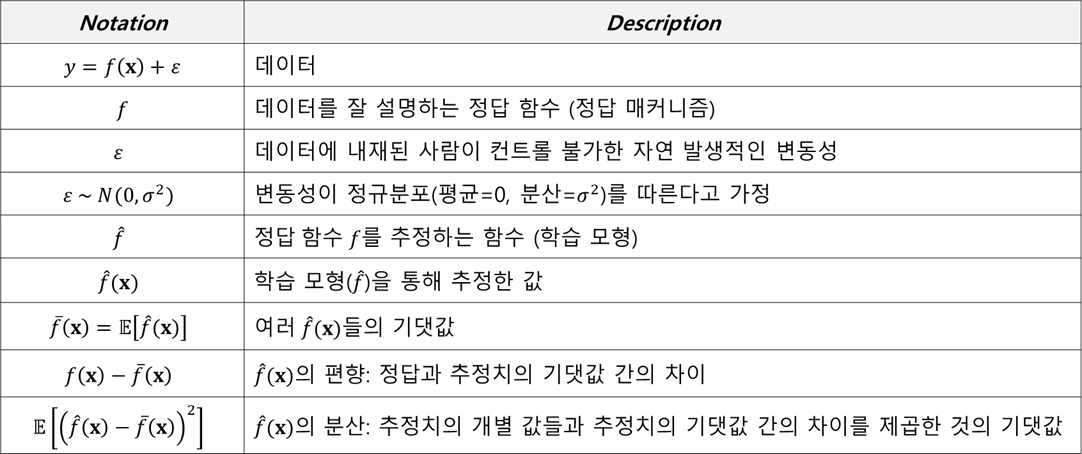
그림3은 데이터로부터 평균 추정치를 도출하는 과정을 도식화한 것이다. 동일한 f를 가지고 데이터셋을 생성한다고 하자. f는 데이터 x에 대해서 항상 동일한 값을 내뱉는다. 하지만 노이즈는 확률변수이므로 서로 다른 값을 가질 수 있으며, 따라서 다른 노이즈를 기반으로 여러 개의 서로 다른 데이터셋을 생성할 수 있다(그림 2. 파란색 박스). 단, 데이터의 사이즈는 서로 동일하다. 그리고 f 추정 함수 f_hat을 기반으로 여러 데이터셋에 대해 y를 추정한 값 f_hat(x)들을 도출한다(그림 2. 초록색 박스). 여러 데이터셋의 추정 값 f_hat(x)들에 기댓값을 취함으로써 모든 가능한 데이터셋의 평균 추정치를 구하게 된다(그림 3. 빨간색 박스).

3. 편향-분산 분해 (Bias-Variance Decomposition)
그러면 이제 위에서 배운 개념들을 바탕으로 편향-분산 분해 과정을 상세히 들여다 보도록 한다. 가장 대표적인 비용 함수인 MSE(Mean Squared Error)를 가지고 유도해 보도록 하겠다. MSE는 정답에서 추정값을 뺀 것의 제곱한 후 기댓값을 취하는 것이므로, 수식으로 나타내면 아래와 같다.

편향-분산 분해의 결론부터 말하자면, MSE는 최종적으로 f_hat(x) 편향의 제곱, f_hat(x)의 분산, 그리고 노이즈의 분산(sigma^2) 이렇게 세 가지로 분해된다. 결과에 대한 수식이 그림 5이다. 이러한 결과가 나오는 과정을 두 가지 단계로 나눠서 보도록 한다. 1단계는 노이즈의 분산이며, 2단계는 편향의 제곱과 분산 분해 유도 과정이다.
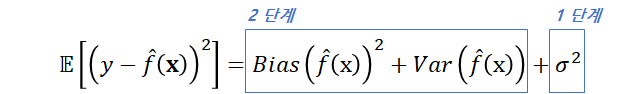
[ 1 단계 ]
우선 첫 번째로, MSE에서 노이즈의 분산을 분해하는 과정을 먼저 보도록 하자. 수식 전개 과정에 의문이 들만한 부분은 빨간색 박스로 부가 설명을 달아 두었다. 마지막을 보면, 수식 오른쪽 끝에 노이즈의 분산이 도출된 것을 볼 수 있다.

[ 2 단계 ]
2단계는 앞서 1단계에서 노이즈의 분산이 아닌 나머지 파란색 부분을 다시 편향의 제곱과 분산으로 분해하는 것이다.

중간에 빨간 색 글씨로, f_hat(x)의 기댓값이 상수라고 했는데, 그 이유는 f_hat(x)가 확률변수이고, 이를 f_hat(x)로 기댓값을 취한 것이기 때문이다. 예를 들면, 확률변수가 X밖에 없을 때, 모든 가능한 X에 대한 기대되는 값을 도출한 것이기 때문에 '변하는 값'이 사라지게 된다. 따라서 기댓값이 상수가 나올 수 있는 것이다.
4. 마치며
이번 포스팅에서는 편향-분산 분해 과정을 유도해보았다. 하지만 분해 결과가 머신러닝에서 어떤 의미를 가지는지, 그리고 앙상블과는 어떻게 연계가 되는 것인지는 언급하지 않았다. 이러한 내용은 앞으로 게시할 포스팅에서 다루도록 하겠다. 스스로 공부하면서 작성한 글이므로, 틀린 부분이 있을 수 있다. 수정할 부분에 대해서는 댓글로 남겨주면 반영하도록 하겠다.
References
[1] https://www.youtube.com/watch?v=mZwszY3kQBg
[2] https://towardsdatascience.com/the-bias-variance-tradeoff-8818f41e39e9?gi=4a6368e5a6e5
The Bias-Variance Tradeoff
In this post, we will explain the bias-variance tradeoff, a fundamental concept in Machine Learning, and show what it means in practice…
towardsdatascience.com
'데이터과학' 카테고리의 다른 글
| [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천 (0) | 2021.08.30 |
|---|---|
| [머신러닝] 앙상블 학습 - 2) Bagging (0) | 2021.06.23 |
| [머신러닝] 앙상블 학습 - 1) 배경 (2) | 2021.06.14 |
| [머신러닝] 편향과 분산의 의미 (1) | 2021.06.04 |
| [통계] 커널 밀도 추정 (Kernel Density Estimation) (4) | 2021.04.27 |




댓글