1. Density Esitmation (밀도 추정) 이란?
확률 밀도 추정이란? 관측된 데이터로부터 변수가 가질 수 있는 모든 값의 확률(밀도)를 추정하는 것이다. 확률 밀도 추정 방법은 Parametric과 Non-parametric 두 가지 방법으로 구분할 수 있다.
1) Parametric
관측된 데이터를 바탕으로 관심 대상인 확률 변수가 특정 분포를 따른다는 가정 하에 확률 밀도를 추정하는 방법이다. 첫번째, 관심 대상인 확률 변수의 분포를 우리가 이미 알고 있는 분포 중에서 하나를 가정한다. 두번째, 관측된 데이터로부터 앞에서 정한 분포의 모수를 추정하는 것이다. 이렇듯 데이터로부터 모수를 구함으로써 분포를 추정한다고 하여 모수 추정법이라고 한다. 예를 들자면, 확률 변수가 정규분포를 따른다고 가정한 다음에 관측 데이터로부터 정규분포의 두 모수인 평균과 분산을 구함으로써 분포를 추정하는 방법이 있다.
2) Non-parametric
비모수 추정법은 특정 분포를 가정하지 않기 때문에 모수를 구하지 않고도 확률밀도를 추정할 수 있는 방법이다. 가장 대표적인 방법은 히스토그램이 있다. 이는 데이터로부터 히스토그램을 구한 후 정규화하여 확률 밀도 함수를 도출하는 과정을 거친다. 그러나 히스토그램 기반의 밀도 추정 방법은 아래와 같은 한계점이 존재한다.
- 계급구간(bin)의 경계가 불연속적 (discrete)
- 계급구간(bin)의 시작 위치에 따라 히스토그램(분포)가 달라짐
- 계급구간(bin)의 크기에 따라 히스토그램(분포)가 달라짐
- 그 외에도 고차원 데이터에 대해서는 메모리 문제 등으로 사용하기 어렵다는 단점이 있음
이러한 히스토그램의 한계점을 일부 개선한 방법이 커널 밀도 추정이다. 커널 밀도 추정은 아래 두 가지 특성을 가지기 때문에 히스토그램의 단점을 개선할 수 있다. 1번과 2번은 각각 히스토그램의 첫번째와 두번째 한계점을 개선할 수 있다.
- KDE는 연속성을 가진 커널 함수를 활용
- 시작 위치의 개념이 없으며, 각 데이터 포인트를 중심(center)으로 하는 커널 함수를 생성
2. Kernel Function (커널 함수) 란?
커널 함수란 다음 3가지 조건을 모두 만족하는 함수를 의미한다. (1) 적분값이 1이며, (2) 원점을 중심으로 대칭인 (3) Non-negative인 경우, 이를 커널 함수라고 한다.
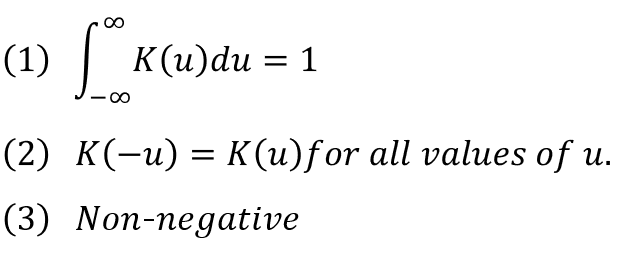
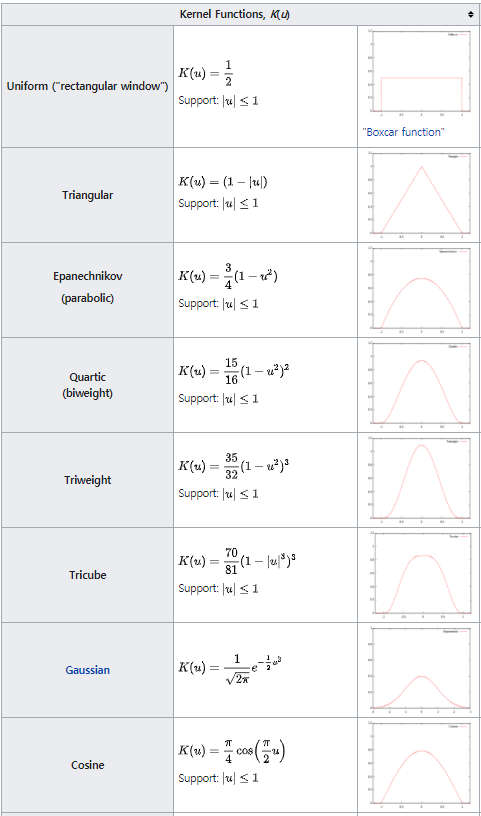
커널의 종류는 다양하며 위키피디아에 잘 설명되어 있다. 아래 사진은 본 글에서 작성자가 코드로 구현한 커널 함수에 대해서만 포함하였다.
3. Kernel Density Estimation (커널 밀도 추정) 이란?
KDE는 커널 함수와 데이터를 바탕으로 연속성 있는 확률 밀도 함수를 추정하는 것이다. 아래 수식을 간단히 설명해 보자면, 관측된 데이터마다 해당 데이터를 중심으로 하는 커널 함수를 생성한 후, 해당 커널 함수를 모두 더하고 데이터 개수로 나누면 KDE로 도출된 확률밀도함수를 구할 수 있다. 아래 수식에서 x는 확률 변수를 의미하고, x_i는 관측된 데이터 포인트 하나를 의미한다.
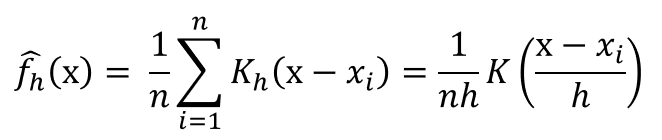
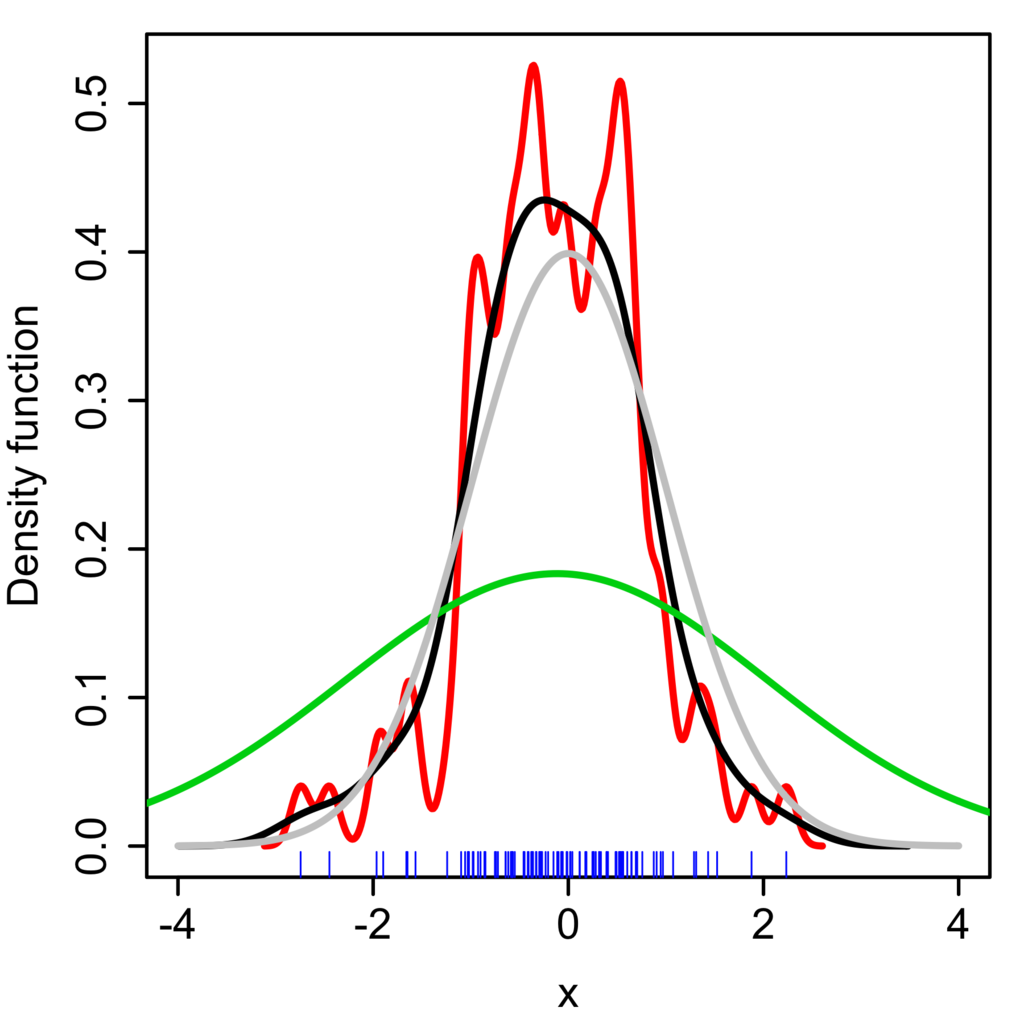
위의 수식에서 h값이 대역폭(bandwidth)를 결정하는 파라미터이다. 대역폭은 확률밀도함수를 스무딩(smoothing)하는 역할을 하며, 대역폭의 값이 작을수록 KDE의 모양이 뾰족하고 클수록 완만한 형태를 띠게 된다. 아래의 위키피디아 예시에서 대역폭에 따른 KDE의 형태를 비교하여 볼 수 있다.
- 빨간색 선: h=0.05
- 검은색 선: h=0.337
- 초록색 선: h=2
4. 예시
아래 6개의 데이터를 바탕으로 밀도를 추정한다고 하자.

커널 함수는 정규 분포로, 대역폭(Bandwidth)은 1로 정한다. 커널을 통해 첫 번째 데이터 값 -2.1을 중심으로 한 정규 분포 모양의 커널 함수를 생성한다. 나머지 5개의 데이터에 대해서도 동일한 작업을 진행한다. 총 6개의 커널 함수들(초록색 실선)을 모두 더한 후 전체 데이터 개수(6개)로 나눈다. 그러면 아래 그림과 같은 결과가 나온다.
- 파란색 실선: 커널 밀도 추정 결과
- 초록색 실선: 각 데이터 값의 커널 함수
- 빨간색 눈금: 각 데이터 값의 위치

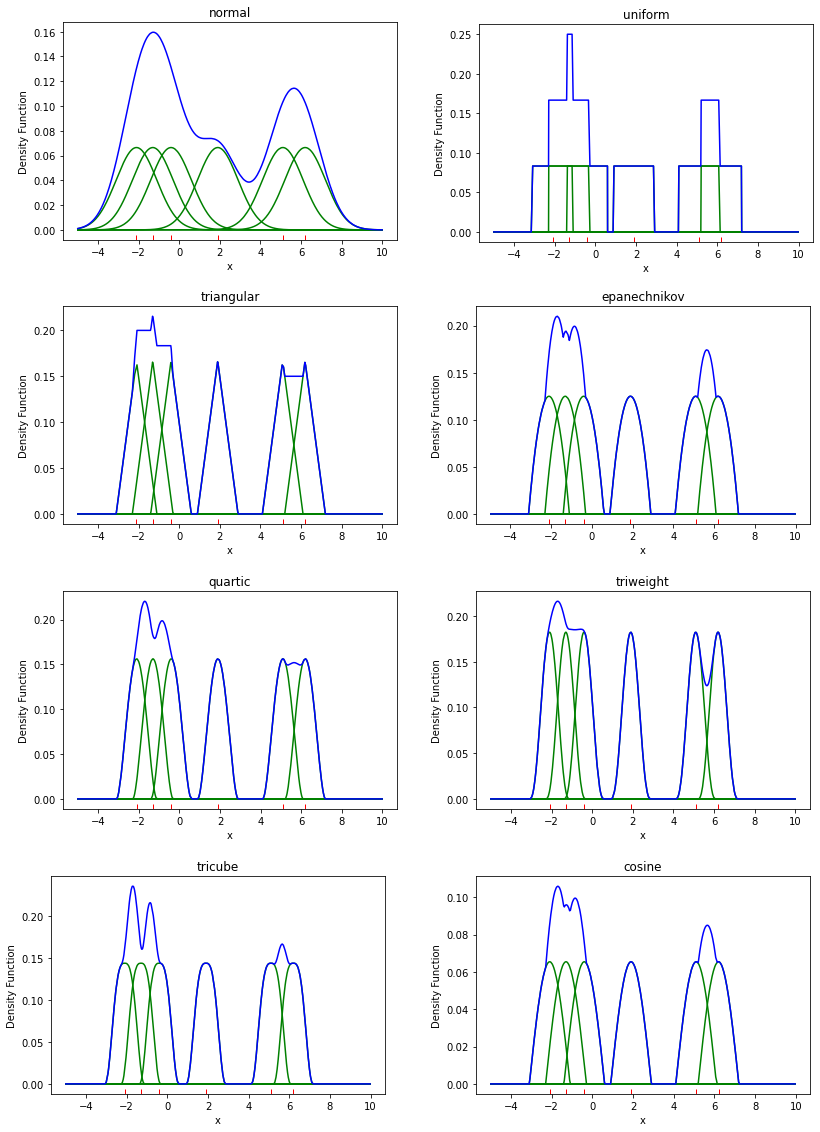
1) 커널 함수 별 KDE 결과
아래는 위와 동일한 데이터와 대역폭일 때, 각 커널 함수에 따른 KDE 결과를 나타낸다.
2) 대역폭 변화에 따른 KDE 결과
아래는 동일한 데이터와 커널 함수(정규분포)일 때, 대역폭에 따른 KDE 결과를 나타낸다.

5. Python Code
아래는 작성자가 직접 구현한 커널 밀도 추정 파이썬 코드이다. 지원하는 라이브러리가 많지만 이해를 돕기 위해 라이브러리를 사용하지 않고 직접 알고리즘을 구현하였다. 여러 커널 함수를 definition으로 정의하여, 커널 함수 종류에 따른 밀도 추정 결과를 쉽게 확인할 수 있도록 구현하였다.
import random
import numpy as np
import seaborn as sns
data = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
h = 5
kernel = 'normal'
len_array = 1000
p_x = np.zeros(len_array)
x = np.array(sorted(np.random.uniform(-5, 10, len_array)))
for x_i in data:
u = (x - x_i)/h
p_x_i = np.array(kernel_function(kernel, u))/len(data)
p_x += p_x_i
sns.lineplot(x=x, y=p_x_i, color='green', linestyle='--')
sns.lineplot(x=x, y=p_x, color='blue').set(title='{} (h={})'.format(kernel, h), xlabel='x', ylabel='Density Function')
sns.rugplot(data, height=0.02, color='red')
def kernel_function(kernel, u):
if kernel == 'normal':
return normal_kernel(u)
elif kernel == 'uniform':
return uniform_kernel(u)
elif kernel == 'triangular':
return triangular_kernel(u)
elif kernel == 'epanechnikov':
return epanechnikov_kernel(u)
elif kernel == 'quartic':
return quartic_kernel(u)
elif kernel == 'triweight':
return triweight_kernel(u)
elif kernel == 'tricube':
return tricube_kernel(u)
elif kernel == 'cosine':
return cosine_kernel(u)
else:
print("[ERROR] Incorrect Kernel Function Name")
def normal_kernel(u):
return np.exp(-(np.abs(u)**2)/2)/(h*np.sqrt(2*np.pi))
def uniform_kernel(u):
return np.where(np.abs(u)<=1,1,0)/2
def triangular_kernel(u):
return (1-np.abs(u))*np.where(np.abs(u)<=1,1,0)
def epanechnikov_kernel(u):
return (3*(1-u**2)*np.where(np.abs(u)<=1,1,0))/4
def quartic_kernel(u):
return ((15*((1-u**2)**2))*np.where(np.abs(u)<=1,1,0))/16
def triweight_kernel(u):
return ((35*((1-u**2)**3))*np.where(np.abs(u)<=1,1,0))/32
def tricube_kernel(u):
return ((70*((1-np.abs(u)**3)**3))*np.where(np.abs(u)<=1,1,0))/81
def cosine_kernel(u):
return (np.pi*np.cos(np.pi*u/2)*np.where(np.abs(u)<=1,1,0)/2)/4
References
[1] en.wikipedia.org/wiki/Kernel_(statistics)#Kernel_functions_in_common_use
Kernel (statistics) - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Window function The term kernel is used in statistical analysis to refer to a window function. The term "kernel" has several distinct meanings in different branches of statistics. Baye
en.wikipedia.org
[2] seongkyun.github.io/study/2019/02/03/KDE/
Kernel Density Estimation (커널 밀도 추정) · Seongkyun Han's blog
Kernel Density Estimation (커널 밀도 추정) 03 Feb 2019 | kernel density estimation KDE 커널 밀도 추정 Kernel Density Estimation (커널 밀도 추정) CNN을 이용한 실험을 했는데 직관적으로는 결과가 좋아졌지만 왜 좋아
seongkyun.github.io
[3] jayhey.github.io/novelty%20detection/2017/11/08/Novelty_detection_Kernel/
커널 밀도 추정(Kernel density estimation) - Parzen window density estimation
다른 밀도 추정법들이 데이터가 특정 분포를 따른다는 가정 하에 추정하는 방법이었습니다. 하지만 이번에 설명할 커널 밀도 추정은 데이터가 특정 분포를 따르지 않는다는 가정 하에 밀도를
jayhey.github.io
KDE(kernel density estimation)
WHAT? Density estimation(밀도추정) 이란 무엇인가? -변수와 데이터 변수 : 모든 값을 가질 수 있는 실체 입니다. 예를들면 나무의 색 이라는 변수가 있습니다. 이 변수에는 수많은 색이 올 수 있습니다
johngiraffe.tistory.com
'데이터과학' 카테고리의 다른 글
| [추천시스템] 비개인화 추천 알고리즘 - 인기도 기반 추천 (0) | 2021.08.30 |
|---|---|
| [머신러닝] 앙상블 학습 - 2) Bagging (0) | 2021.06.23 |
| [머신러닝] 앙상블 학습 - 1) 배경 (2) | 2021.06.14 |
| [머신러닝] 편향과 분산의 의미 (1) | 2021.06.04 |
| [머신러닝] 편향-분산 분해 (Bias-Variance Decomposition) (2) | 2021.05.29 |




댓글